弧度

  提示：本条目的主题不是曲率。

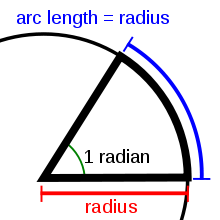
單位弧度

常見的各種弧度

弧度又稱弳度，是平面角的單位，也是國際單位制導出單位。單位弧度定義為圓弧長度等於半徑時的圓心角。角度以弧度給出時，通常不寫弧度單位，或有時記為rad（㎭）。平面角和立體角皆無因次。

一個完整的圓的弧度是2π{displaystyle 2pi }，所以2π{displaystyle 2pi }rad = 360°，π{displaystyle pi }rad = 180°，1°=π180∘{displaystyle {frac {pi }{180^{circ }}}}rad，1 rad = 180∘π{displaystyle {frac {180^{circ }}{pi }}}（約57.29577951°）。以度數表示的角度，把數字乘以π180∘{displaystyle {frac {pi }{180^{circ }}}}便轉換成弧度；以弧度表示的角度，乘以180∘π{displaystyle {frac {180^{circ }}{pi }}}便轉換成度數。

π180×deg=rad{displaystyle {frac {pi }{180}}times deg=rad}

同樣地︰

deg=rad×180π{displaystyle deg=radtimes {frac {180}{pi }}}

微積分的三角函數中，角度以弧度為單位，以獲得簡潔的結果。例如以弧度為單位，有如下簡單等式：

limh→0sin⁡hh=1{displaystyle lim _{hto 0}{frac {sin h}{h}}=1}，

從這等式可以推導出很多漂亮的數學等式。

把三角函數寫成泰勒级数，則必須以弧度表示。

sin⁡x=∑n=0∞(−1)n(2n+1)!x2n+1=x−x33!+x55!−⋯{displaystyle sin x=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-cdots quad !}

相同角度的轉換表

角度單位	值
轉	0{displaystyle 0}	112{displaystyle {frac {1}{12}}}	18{displaystyle {frac {1}{8}}}	16{displaystyle {frac {1}{6}}}	14{displaystyle {frac {1}{4}}}	12{displaystyle {frac {1}{2}}}	34{displaystyle {frac {3}{4}}}	1{displaystyle 1}
角度	0∘{displaystyle 0^{circ }}	30∘{displaystyle 30^{circ }}	45∘{displaystyle 45^{circ }}	60∘{displaystyle 60^{circ }}	90∘{displaystyle 90^{circ }}	180∘{displaystyle 180^{circ }}	270∘{displaystyle 270^{circ }}	360∘{displaystyle 360^{circ }}
弧度	0{displaystyle 0}	π6{displaystyle {frac {pi }{6}}}	π4{displaystyle {frac {pi }{4}}}	π3{displaystyle {frac {pi }{3}}}	π2{displaystyle {frac {pi }{2}}}	π{displaystyle pi }	3π2{displaystyle {frac {3pi }{2}}}	2π{displaystyle 2pi }
梯度	0g{displaystyle 0^{g}}	3313g{displaystyle 33{frac {1}{3}}^{g}}	50g{displaystyle 50^{g}}	6623g{displaystyle 66{frac {2}{3}}^{g}}	100g{displaystyle 100^{g}}	200g{displaystyle 200^{g}}	300g{displaystyle 300^{g}}	400g{displaystyle 400^{g}}

參見

• 角度


• 球面度

參考文獻

.mw-parser-output .refbegin{font-size:90%;margin-bottom:0.5em}.mw-parser-output .refbegin-hanging-indents>ul{list-style-type:none;margin-left:0}.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>dd{margin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none}.mw-parser-output .refbegin-100{font-size:100%}

• ISO 31-1


• ISO/IEC 80000-3

外部連結

維基教科書中的相關電子教程：Trigonometry/Radian and degree measures

查询維基詞典中的radian。

• 
  Radian at MathWorld
  

查 论 编 国际单位 基本单位 秒 米 千克 开尔文 安培 坎德拉 摩尔 导出单位 赫茲 弧度 球面度 牛頓 帕斯卡 焦耳 瓦特 庫侖 伏特 歐姆 法拉 西门子 韋伯 特斯拉 亨利 摄氏度 流明 勒克斯 贝克勒尔 戈瑞 希沃特 開特 可并用單位 天文單位 吨 原子質量單位 升 分 小时 天 度 角分 角秒 电子伏 分貝 公頃 奈培 原子單位 自然單位 參閱 计量单位 计量单位制 单位换算 國際單位制詞頭 2019年國際單位制基本單位的重新定義 分类:國際單位制基本單位 分类:国际单位制导出单位

查 论 编 经典力学国际单位 线性（平动）的量 角度（转动）的量 量纲 — L L2 量纲 — — — T 时间: .mw-parser-output .serif{font-family:Times,serif} t s absement（英语：absement）: A m s（英语：meter second） T 时间: t s — 距离: d, 位矢: r, s, x, 位移 m 面积: A m2 — 角度: θ, 角移: θ rad 立體角: Ω rad2, sr T−1 頻率: f s−1（英语：inverse second）, Hz 速率: v, 速度: v m s−1 面積速率: ν, 比角动量（英语：specific angular momentum）: h m2 s−1 T−1 頻率: f s−1（英语：inverse second）, Hz 角速率: ω, 角速度: ω rad s−1 T−2 加速度: a m s−2 T−2 角加速度: α rad s−2 T−3 加加速度: j m s−3 T−3 角加加速度: ζ rad s−3 M 质量: m kg ML2 转动惯量:  I kg m2 MT−1 动量: p, 冲量: J kg m s−1, N s（英语：newton second） 作用量: 𝒮, actergy（英语：actergy）: ℵ kg m2 s−1, J s（英语：joule-second） ML2T−1 角动量: L, 角冲量: ΔL kg m2 s−1 作用量: 𝒮, actergy（英语：actergy）: ℵ kg m2 s−1, J s（英语：joule-second） MT−2 力: F, 重量: Fg kg m s−2, N 能量: E, 功: W kg m2 s−2, J ML2T−2 力矩: τ, moment（英语：Moment (physics)）: M kg m2 s−2, N m 能量: E, 功: W kg m2 s−2, J MT−3 yank（英语：List_of_equations_in_classical_mechanics#Dynamics）: Y kg m s−3, N s−1 功率: P kg m2 s−3, W ML2T−3 rotatum（英语：rotatum）: P kg m2 s−3, N m s−1 功率: P kg m2 s−3, W

This page is only for reference, If you need detailed information, please check here