双曲线

在数学中，双曲线（希臘語：ὑπερβολή，意思是超过、超出）是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

它还可以定义为与两个固定的点（称为焦点）的距离差是常数的点的轨迹。这个固定的距离差是a{displaystyle a}的两倍，这里的a{displaystyle a}是从双曲线的中心到双曲线最近的分支的顶点的距离。a{displaystyle a}还称为双曲线的半实轴。焦点位于贯轴上，它们的中间点称为中心。

从代数上说，双曲线是在笛卡尔平面上由如下方程定义的曲线

Ax2+Bxy+Cy2+Dx+Ey+F=0{displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}

使得B2>4AC{displaystyle B^{2}>4AC}，这裡的所有系数都是实数，并存在定义在双曲线上的点对(x,y){displaystyle (x,y)}的多于一个的解。

注意在笛卡尔坐标平面上两个互为倒数的变量的图像是双曲线。

• 等轴双曲线：双曲线的实轴与虚轴长相等，即2a=2b{displaystyle 2a=2b}且e=2{displaystyle e={sqrt {2}}}，此时渐近线方程为y=±x{displaystyle y=pm x}（无论焦点在x{displaystyle x}轴还是y{displaystyle y}轴）。

• 共轭双曲线：双曲线S′{displaystyle S'}的实轴是双曲线S{displaystyle S}的虚轴且双曲线S′{displaystyle S'}的虚轴是双曲线S{displaystyle S}的实轴时，称双曲线S′{displaystyle S'}与双曲线S{displaystyle S}为共轭双曲线。

几何表达：{S:x2a2−y2b2=1S′:y2b2−x2a2=1{displaystyle {begin{cases}S:{frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1\S':{frac {y^{2}}{b^{2}}}-{frac {x^{2}}{a^{2}}}=1\end{cases}}}

特点：

1. 共渐近线，与渐近线平行的直线和双曲线有且只有一个交点。


2. 焦距相等。


3. 两双曲线的离心率平方后的倒数相加等于1{displaystyle 1}。

• 单位双曲线：属于等轴双曲线，且半实轴和半虚轴的长均为1{displaystyle 1}，即a=b=2{displaystyle a=b=2}。

满足方程：x2−y2=1{displaystyle x^{2}-y^{2}=1}或y2−x2=1{displaystyle y^{2}-x^{2}=1}。

目录

• 
  1 定义
  


• 
  2 笛卡尔坐标
  


• 
  3 极坐标
  


• 
  4 双曲线的参数方程
  


• 
  5 双曲线的标准方程
  


• 
  6 双曲线的渐近线方程
  


• 
  7 圆锥曲线方程
  


• 
  8 参考文献
  


• 
  9 外部链接
  


• 
  10 参见
  

定义

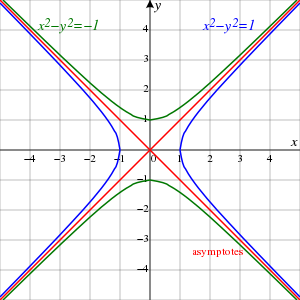
共轭单位直角双曲线

前两个上面已经列出了：

• 平面切直角圆锥面的两半的交截线。


• 与两个固定点（称为焦点）距离差为常数的点的轨迹。


• 到一个焦点的距离和到一条直线（称为准线）的距离的比例是大于1{displaystyle 1}的常数的点的轨迹。这个常数称为双曲线的偏心率。

双曲线由分开两个焦点的两个分离的称为臂或分支的曲线构成。随着到焦点的距离的变大，双曲线就越逼近称为渐近线的两条线。渐近线交叉于双曲线的中点，并对于东西开口的双曲线有斜率±ba{displaystyle pm {frac {b}{a}}}，对于北南开口的双曲线有斜率±ab{displaystyle pm {frac {a}{b}}}。

双曲线有个性质，出自一个焦点的射线反射于双曲线后看起来像是出自另一个焦点。

双曲线的一个特殊情况是“等轴”或“直角”双曲线，它的渐近线交于直角。以坐标轴作为渐近线的直角双曲线由方程xy=c{displaystyle xy=c}给出，这裡的c{displaystyle c}是常数。

如同正弦和余弦函数给出椭圆的参数方程，双曲函数给出双曲线的参数方程。

如果对双曲线方程交换x{displaystyle x}和y{displaystyle y}，得到它的共轭双曲线。共轭双曲线有同样的渐近线。

笛卡尔坐标

中心位于(h,k){displaystyle (h,k)}的左右开口的双曲线：

(x−h)2a2−(y−k)2b2=1{displaystyle {frac {left(x-hright)^{2}}{a^{2}}}-{frac {left(y-kright)^{2}}{b^{2}}}=1}

中心位于(h,k){displaystyle (h,k)}的上下开口的双曲线：

(y−k)2a2−(x−h)2b2=1{displaystyle {frac {left(y-kright)^{2}}{a^{2}}}-{frac {left(x-hright)^{2}}{b^{2}}}=1}

实轴贯穿双曲线的中心并交双曲线两臂于它们的顶点（拐点）。焦点位于双曲线实轴的延长线上。虚轴贯穿双曲线中点并垂直于实轴。

在两个公式中，a{displaystyle a}是半实轴（在双曲线两臂之间沿着实轴测量的距离），而b{displaystyle b}是半虚轴。

如果用双曲线的两个顶点的切线交渐近线形成一个矩形，在切线上的两边的长度是2b{displaystyle 2b}，平行于实轴的两边的长度是2a{displaystyle 2a}，注意b{displaystyle b}可以大于a{displaystyle a}。

如果计算从双曲线上任意准线上的点到每个焦点的距离，这两个距离的差的绝对值总是2a{displaystyle 2a}。

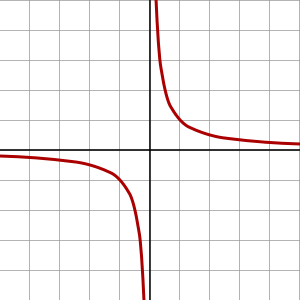
直角双曲线y=1x{displaystyle y={tfrac {1}{x}}}的图像。

离心率给出自：

e=1+b2a2{displaystyle e={sqrt {1+{frac {b^{2}}{a^{2}}}}}}

左右开口的双曲线的焦点是：(h±c,k){displaystyle left(hpm c,kright)}，其中c给出自c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2}}。

上下开口的双曲线的焦点是：(h,k±c){displaystyle left(h,kpm cright)}，其中c给出自c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2}}。

对于以直线x=h{displaystyle x=h}和直线y=k{displaystyle y=k}为渐近线的直角双曲线：

(x−h)(y−k)=c{displaystyle (x-h)(y-k)=c}

这种双曲线最简单的例子是：

y=mx{displaystyle y={frac {m}{x}}}

极坐标

左右开口的双曲线：

r2=a2sec⁡2θ{displaystyle r^{2}=a^{2}sec {2}theta }

上下开口的双曲线：

r2=−a2sec⁡2θ{displaystyle r^{2}=-a^{2}sec {2}theta }

上右下左开口的双曲线：

r2=a2csc⁡2θ{displaystyle r^{2}=a^{2}csc {2}theta }

上左下右开口的双曲线：

r2=−a2csc⁡2θ{displaystyle r^{2}=-a^{2}csc {2}theta }

在所有公式中，中心在极点，而a{displaystyle a}是半实轴和半虚轴。

双曲线的参数方程

左右开口的双曲线：

{x=asec⁡t+hy=btan⁡t+k{displaystyle {begin{cases}x=asec {t}+h\y=btan {t}+k\end{cases}}}

或

{x=acosh⁡t+hy=bsinh⁡t+k{displaystyle {begin{cases}x=acosh {t}+h\y=bsinh {t}+k\end{cases}}}

上下开口的双曲线：

{x=atan⁡t+hy=bsec⁡t+k{displaystyle {begin{cases}x=atan {t}+h\y=bsec {t}+k\end{cases}}}

或

{x=asinh⁡t+hy=bcosh⁡t+k{displaystyle {begin{cases}x=asinh {t}+h\y=bcosh {t}+k\end{cases}}}

在所有公式中，(h,k){displaystyle (h,k)}是双曲线的中点，a{displaystyle a}是半实轴而b{displaystyle b}是半虚轴。

双曲线的标准方程

焦点在x{displaystyle x}轴：x2a2−y2b2=1{displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1}

焦点在y{displaystyle y}轴：y2a2−x2b2=1{displaystyle {frac {y^{2}}{a^{2}}}-{frac {x^{2}}{b^{2}}}=1}

双曲线的渐近线方程

焦点在x{displaystyle x}轴：y=±bax{displaystyle y=pm {frac {b}{a}}x}

焦点在y{displaystyle y}轴：y=±abx{displaystyle y=pm {frac {a}{b}}x}

圆锥曲线方程

ρ=ep1+ecos⁡θ{displaystyle rho ={frac {ep}{1+ecos theta }}}

当e>1{displaystyle e>1}时，表示双曲线。其中p{displaystyle p}为焦点到准线距离，θ{displaystyle theta }为弦与x{displaystyle x}轴夹角。

参考文献

外部链接

• 
  PlanetMath上Unit hyperbola的資料。


• 
  PlanetMath上Conic section的資料。


• 
  PlanetMath上Conjugate hyperbola的資料。


• Mathworld - Hyperbola

参见

• 圆锥曲线


• 双曲函数

查 论 编 几何学术语 點 頂點 交點 中點 角 直線和曲線 線段 射線 直線 切線 法线 曲線 圓錐曲線 双曲线 抛物线 螺線 邊 周界 弦 弧 垂直平分線 平面圖形 圓 橢圓 扇形 弓形 多邊形 三角形 四邊形 五边形 六边形 多边形 梯形 平行四邊形 菱形 矩形 正方形 鷂形 卵形线 立體圖形 多面體 正多面體 四面体 長方體 立方體 平行六面体 棱柱 反棱柱 棱錐 圓柱體 圓錐 圓台 橢球 球體 球缺 球冠 球台 二次曲面 抛物面 雙曲面 圖形關係 相似 全等 对称 平行 垂直 相交 相切 镜像 旋转 反演 三角形關係 相似三角形 全等三角形 量 距離 長度 周长 弧长 高度 面積 表面積 體積 容積 角度 作圖 尺 直尺 三角尺 圓規 尺規作圖 二刻尺作图 理論 定理 公理 定义 證明 分类 主题 共享资源 专题

规范控制 AAT: 300163048 GND: 4161034-9

This page is only for reference, If you need detailed information, please check here