黎曼球面

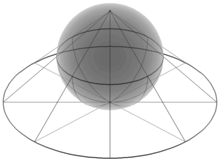
黎曼球面可以视为复数平面（通过某种下文有详细介绍的立体投影）包在一个球外面。

数学上，黎曼球面是一种将複數平面加上一个无穷远点的扩张，使得下面这类公式至少在某种意义下有意义

1/0=∞.{displaystyle 1/0=infty .}

它由19世纪数学家黎曼而得名。也称为

• 
  複射影直线，记为 CP1{displaystyle mathbb {CP} ^{1}}，和


• 
  扩充复平面，记为 C^{displaystyle mathbb {hat {C}} }或者C∪{∞}{displaystyle mathbb {C} cup {infty }}.

从纯代数的角度，复数加上一个无穷远点构成一个数系称为扩充复数。无穷远点的算数有时和一般的代数规则不符，因此扩充复数不构成一个代数域。但是，黎曼球面在几何和解析角度都行为良好，甚至在无穷远点也不例外；它是一个一维复流形，也称黎曼曲面。

复分析中，黎曼球面对于亚纯函数这个优雅的理论很有帮助。黎曼球面在射影几何和代数几何中作为复流形、射影空间和代数簇的基本例子到处出现。它在涉及分析和几何的其他学科也很有用，譬如量子力学和物理学其他分支。

目录

• 
  1 作为复流形
  


• 
  2 作为複射影线
  


• 
  3 作为球面
  


• 
  4 度量
  


• 
  5 自同构
  


• 
  6 应用
  


• 
  7 参考
  


• 
  8 参看
  


• 
  9 外部链接
  

作为复流形

作为一维复流形，黎曼曲面可以由两个图卡描述，每个的定义域都是复数平面C{displaystyle mathbb {C} }.令ζ{displaystyle zeta }和ξ{displaystyle xi }为C{displaystyle mathbb {C} }上的複座标。将非零复数ζ{displaystyle zeta }和非零复数ξ{displaystyle xi }用如下转移映射等同起来：

ζ=1/ξ,{displaystyle zeta =1/xi ,}

ξ=1/ζ.{displaystyle xi =1/zeta .}

因为这些变换映射为全纯函数，他们定义了一个复流形，称为黎曼球面。

直观地来看，这些变换映射表示了如何将两个平面粘合成一个黎曼球面。两个面用一种"从裏翻出来"的方式粘合，所以他们几乎处处重合，每个平面（用自己的原点）贡献对方平面上缺少的一点。换言之，（几乎）所有黎曼球面上的点既有ζ{displaystyle zeta }值也有ξ{displaystyle xi }值，而两个值由ζ=1/ξ{displaystyle zeta =1/xi }关联。ξ=0{displaystyle xi =0}处的点应该具有ζ{displaystyle zeta }值 "1/0{displaystyle 1/0}"；从这个意义上讲，ξ{displaystyle xi }-图的原点是ζ{displaystyle zeta }-图上的"∞{displaystyle infty }"。对称地，ζ{displaystyle zeta }-图的原点对应于ξ{displaystyle xi }-图上的∞{displaystyle infty }.

拓扑上，最后的结果是从平面到球面的单点紧致化。但是，黎曼球面不单单是一个拓扑球面。它是具有复结构的拓扑球面，所以球面上的每个点都有一个领域可以通过双全纯函数和C{displaystyle mathbb {C} }同胚。

另一方面，黎曼曲面分类的的中心结果单值化定理，断言唯一的单连通一维复流形为复平面、双曲平面、和黎曼球面。在这三者中，黎曼球面是唯一的闭曲面（无边界的紧致曲面）。因此二维球面只有唯一的复结构将它变为一维复流形。

作为複射影线

黎曼球面也可以定义为複射影线。这也就是C2{displaystyle mathbb {C} ^{2}}的子集，由所有非零复数对(α,β){displaystyle (alpha ,beta )}构成，模如下等价关系:

(α,β)=(λα,λβ){displaystyle (alpha ,beta )=(lambda alpha ,lambda beta )}

对于所有非零复数λ{displaystyle lambda }成立。复平面C{displaystyle mathbb {C} }用座标ζ{displaystyle zeta }，可以映射到複射影线：

(α,β)=(ζ,1).{displaystyle (alpha ,beta )=(zeta ,1).}

另一个C{displaystyle mathbb {C} }用座标ξ{displaystyle xi }也映射到複射影线

(α,β)=(1,ξ).{displaystyle (alpha ,beta )=(1,xi ).}

这两个复图覆盖整个射影线。对于非零ξ{displaystyle xi }，等同关系：

(1,ξ)=(1/ξ,1)=(ζ,1){displaystyle (1,xi )=(1/xi ,1)=(zeta ,1)}

给出了变换映射ζ=1/ξ{displaystyle zeta =1/xi }和ξ=1/ζ{displaystyle xi =1/zeta }，同上文一致。

这个黎曼球面的定义和射影几何直接相关。例如任何複射影平面上的直线(或者光滑圆锥曲线)双全纯等价于复射影线。这个表达对于研究下文所述的球面的自同构也很方便。

作为球面

从复数A{displaystyle A}到黎曼球面上的一点α{displaystyle alpha }的球极投影。

黎曼球面可以显示为三维实空间R3{displaystyle mathbb {R} ^{3}}中的单位球面x2+y2+z2=1{displaystyle x^{2}+y^{2}+z^{2}=1}.为此，考虑从单位球减去一点(0,0,1){displaystyle (0,0,1)}到（赤道）平面z=0{displaystyle z=0}的球极投影，可以将该平面等同于复平面ζ=x+iy{displaystyle zeta =x+iy}.在笛卡尔坐标系(x,y,z){displaystyle (x,y,z)}和球面坐标系(ϕ,θ){displaystyle (phi ,theta )}中（其中ϕ{displaystyle phi }为天顶角而θ{displaystyle theta }为方位角)，该投影为

ζ=x+iy1−z=cot⁡(φ/2)eiθ.{displaystyle zeta ={frac {x+iy}{1-z}}=cot(varphi /2);e^{itheta }.}

类似的，从(0,0,−1){displaystyle (0,0,-1)}到z=0{displaystyle z=0}平面的球极投影将另一份复平面ξ=x−iy{displaystyle xi =x-iy}等同于赤道平面，记为

ξ=x−iy1+z=tan⁡(φ/2)e−iθ.{displaystyle xi ={frac {x-iy}{1+z}}=tan(varphi /2);e^{-itheta }.}

(两份复平面和平面z=0{displaystyle z=0}的对应方式不同。必须使用定向翻转来保证球面上定向的一致性，实际上复共轭使得变换映射成为全纯函数。）ζ{displaystyle zeta }-座标和ξ{displaystyle xi }-座标之间的变换函数可以通过将其中一个映射和另一个的逆的复合得到。它们就是如上所述的ζ=1/ξ{displaystyle zeta =1/xi }和ξ=1/ζ{displaystyle xi =1/zeta }。因此单位球面和黎曼球面微分同胚。

在这个微分同胚下，ζ{displaystyle zeta }-图中的单位圆，ξ{displaystyle xi }-图中的单位圆，以及单位球面的赤道可以等同起来。单位圆盘|ζ|<1{displaystyle |zeta |<1}和南半球面z<0{displaystyle z<0}，单位圆盘|ξ|<1{displaystyle |xi |<1}和北半球面z>0{displaystyle z>0}分别等同。

度量

黎曼曲面没有特定的黎曼度量。但是，黎曼曲面的复结构的确在共形等价下确定了唯一的度量。（两个度量称为共形等价，如果他们的区别只是一个正光滑函数的因子。）反过来，可定向曲面上的任意度量唯一的决定一个复结构，该结构在共形等价下依赖于该度量。因此可定向曲面的复结构和该曲面上的度量的共形类有一一对应。

给定共形类，可以用共形对称性找到一个有合适属性的代表度量。精确地讲，每个共形类总是有一个常曲率完备度量。

在黎曼球面的情况，高斯-博内定理表明常曲率度量必须有正的曲率K。因而该度量必须通过球极投影等度于R3{displaystyle mathbb {R} ^{3}}中半径为1/K{displaystyle 1/{sqrt {K}}}的球面。对于黎曼球面上的ζ{displaystyle zeta }-图，K=1{displaystyle K=1}度量可以给出如下：

ds2=(21+|ζ|2)2|dζ|2=4(1+ζζ¯)2dζdζ¯.{displaystyle ds^{2}=left({frac {2}{1+|zeta |^{2}}}right)^{2},|dzeta |^{2}={frac {4}{left(1+zeta {bar {zeta }}right)^{2}}},dzeta d{bar {zeta }}.}

在实座标ζ=u+iv{displaystyle zeta =u+iv}中，该公式为：

ds2=4(1+u2+v2)2(du2+dv2).{displaystyle ds^{2}={frac {4}{left(1+u^{2}+v^{2}right)^{2}}}left(du^{2}+dv^{2}right).}

除了一个常数因子，该度量和复射影空间（黎曼球面就是一个特例）中的富比尼-施图迪度量一样。

反过来，令S代表（作为微分流形或者拓扑流形的）球面。按照单值化定理，存在唯一的S上的复结构。由此可见，S上的度量和球面度量共形等价。所有这样的度量构成一个共形类。因此"圆球"度量不是黎曼球面的内在度量，因为"圆形"并不是共形几何的不变量。黎曼球面只是一个共形流形而非黎曼流形。但是，如果需要用到黎曼球面上的黎曼度量，圆形度量是一个很自然的选择。

自同构

作用于球面上以及作用于球极投影的平面上的莫比乌斯变换。

主条目：莫比乌斯变换

理解数学对象的自同构群有助于对该对象的研究，自同构也就是对象到自身保持其基本结构不变的映射。对于黎曼球面，自同构就是黎曼球面到自身的可逆双全纯映射。唯一可能的这样的映射只有莫比乌斯变换。这些变换有如下形式：

f(ζ)=aζ+bcζ+d,{displaystyle f(zeta )={frac {azeta +b}{czeta +d}},}

其中a{displaystyle a}、b{displaystyle b}、c{displaystyle c}、和d{displaystyle d}为复数，满足ad−bc≠0{displaystyle ad-bcneq 0}.莫比乌斯变换的例子包括膨胀，旋转，平移，和复倒数。事实上，所有莫比乌斯变换可以有这些特例的复合得到。

将莫比乌斯变换视作复射影线上的变换很有益。在射影座标下，变换f{displaystyle f}可以写作

f(α,β)=(aα+bβ,cα+dβ)=(αβ)(acbd).{displaystyle f(alpha ,beta )=(aalpha +bbeta ,calpha +dbeta )={begin{pmatrix}alpha &beta end{pmatrix}}{begin{pmatrix}a&c\b&dend{pmatrix}}.}

这样，莫比乌斯变换可以表述为行列式非零的2×2{displaystyle 2times 2}复矩阵；两个矩阵产生同样的莫比乌斯变换当且仅当他们只差一个非零常数。这样莫比乌斯变换恰好对应于射影线性变换PGL2(C){displaystyle mathrm {PGL} _{2}(mathbb {C} )}.

如果赋予黎曼球面富比尼-施图迪度量，则不是所有的莫比乌斯变换是等度的；例如膨胀和平移就不是。等度变换构成PGL2(C){displaystyle mathrm {PGL} _{2}(mathbb {C} )}的一个子群，也即PSU2{displaystyle mathrm {PSU} _{2}}.该子群同构于旋转群SO(3){displaystyle mathrm {SO} (3)}，它是单位球在R3{displaystyle mathbb {R} ^{3}}中的等度群。

应用

复分析中，复平面（或者任何黎曼曲面）上的的亚纯函数是两个全纯函数f{displaystyle f}和g{displaystyle g}的比值f/g{displaystyle f/g}.作为到复数的映射，任何g{displaystyle g}为零的地方，它就没有定义。但是，它引出了一个全纯映射(f,g){displaystyle (f,g)}到复射影线，甚至在g=0{displaystyle g=0}处也有定义。这个构造对于研究全纯和亚纯函数很有用。例如，紧致黎曼曲面上不存在存在非常数复值全纯映射，但是有很多到复射影线上的全纯映射。

黎曼球面有很多物理中的应用。量子力学中，复射影线上的点是光子极化态，自旋为1/2的重亚原子粒子和一般二态粒子的的自旋态的自然取值。黎曼球面被推荐为天体球面的广义相对论模型。弦论中，弦的世界面是黎曼曲面，而黎曼球面作为最简单的黎曼曲面有重要的作用。它在扭子理论中也很重要。

参考

• 
  Brown, James and Churchill, Ruel. Complex Variables and Applications. New York: McGraw-Hill. 1989. ISBN 0070109052. 
  


• 
  Griffiths, Phillip and Harris, Joseph. Principles of Algebraic Geometry. John Wiley & Sons. 1978. ISBN 0-471-32792-1. 
  


• 
  Penrose, Roger. The Road to Reality. New York: Knopf. 2005. ISBN 0-679-45443-8. 
  


• 
  Rudin, Walter. Real and Complex Analysis. New York: McGraw-Hill. 1987. ISBN 0071002766. 
  

参看

• 共形几何


• 交比


• 霍普夫纤维化


• 儿童画

外部链接

• 
  Twistor Theory^{[永久失效連結]}, R. Penrose和F. Hadrovich


• 
  Moebius Transformations Revealed, Douglas N. Arnold和Jonathan Rogness (两位明尼苏达大学教授所作视频，用球面上的球极投影解释莫比乌斯变换)

This page is only for reference, If you need detailed information, please check here