量子態

設定斯特恩-革拉赫實驗儀器的磁場方向為z-軸，入射的銀原子束可以被分裂成兩道銀原子束，每一道銀原子束代表一種量子態，上旋|↑⟩{displaystyle |uparrow rangle }或下旋|↓⟩{displaystyle |downarrow rangle }。^[1]:1-4

在量子力學裏，量子態（英语：quantum state）指的是量子系統的狀態。態向量可以用來抽象地表示量子態。^[2]:93-96採用狄拉克標記，態向量表示為右矢|ψ⟩{displaystyle |psi rangle }；其中，在符號內部的希臘字母ψ{displaystyle psi }可以是任何符號，字母，數字，或單字。例如，在計算氫原子能譜時，能級與主量子數n{displaystyle n}有關，所以，每個量子態的態向量可以表示為|n⟩{displaystyle |nrangle }。

一般而言，量子態可以是純態或混合態。上述案例是純態。混合態是由很多純態組成的機率混合。不同的組合可能會組成同樣的混合態。當量子態是混合態時，可以用密度矩陣做數學描述，這密度矩陣實際給出的是機率，不是密度。純態也可以用密度矩陣表示。

哥本哈根詮釋以操作定義的方法對量子態做定義：量子態可以從一系列製備程序來辨認，即這程序所製成的量子系統擁有這量子態。^[3]:15-16例如，使用z-軸方向的斯特恩-革拉赫實驗儀器，如右圖所示，可以將入射的銀原子束，依照自旋的z-分量Sz{displaystyle S_{z}}分裂成兩道，一道的Sz{displaystyle S_{z}}為上旋，量子態為|↑⟩{displaystyle |uparrow rangle }或|z+⟩{displaystyle |z+rangle }，另一道的Sz{displaystyle S_{z}}為下旋，量子態為|↓⟩{displaystyle |downarrow rangle }或|z−⟩{displaystyle |z-rangle }，這樣，可以製備成量子態為|↑⟩{displaystyle |uparrow rangle }的銀原子束，或量子態為|↓⟩{displaystyle |downarrow rangle }的銀原子束。^[1]:1-4銀原子自旋態向量存在於二維希爾伯特空間。對於這純態案例，相關的態向量|ψ⟩=α|↑⟩+β|↓⟩{displaystyle |psi rangle =alpha |uparrow rangle +beta |downarrow rangle }是二維複值向量(α,β){displaystyle (alpha ,beta )}，長度為1：

|α|2+|β|2=1{displaystyle |alpha |^{2}+|beta |^{2}=1}。

在測量一個量子系統之前，量子理論通常只給出測量結果的機率分佈，這機率分佈的形式完全由量子態、相關的可觀察量來決定。對於純態或混合態，都可以從密度矩陣計算出這機率分佈。

另外，還有很多種不同的量子力學詮釋。根據實在論詮釋，一個量子系統的量子態完整描述了這個量子系統。量子態囊括了所有關於這系統的描述。實證詮釋闡明，量子態只與對於量子系統做觀察所得到的實驗數據有關。^[3]:15按照系綜詮釋，量子態代表一個系綜的在同樣狀況下製備而成的量子系統，它不適用於單獨量子系統。^[3]:220

目录

• 
  1 概述
  
  
  
  • 
    1.1 經典力學的狀態
    
  
  
  • 
    1.2 量子力學的量子態
    
  
  
  • 
    1.3 薛丁格繪景與海森堡繪景
    
  
  
  
  


• 
  2 量子力學形式論
  
  
  
  • 
    2.1 狄拉克標記
    
  
  
  • 
    2.2 量子態的測量
    
  
  
  • 
    2.3 單粒子系統的基底量子態
    
    
    
    • 
      2.3.1 離散案例
      
    
    
    • 
      2.3.2 連續案例
      
    
    
    
    
  
  
  • 
    2.4 態疊加原理
    
  
  
  
  


• 
  3 參閱
  


• 
  4 註釋
  


• 
  5 參考文獻
  

概述

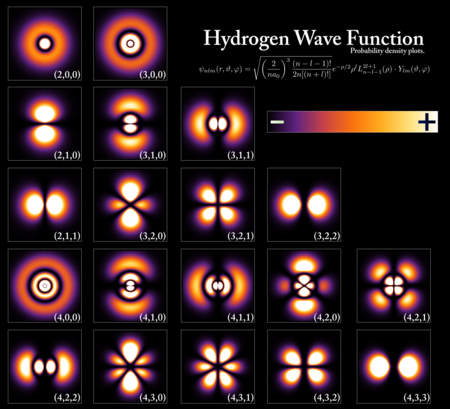
在不同量子态氢原子的电子概率密度。

經典力學的狀態

設想在某經典系統裏，有一個粒子移動於一維空間，在時間t=0{displaystyle t=0}，粒子的位置q{displaystyle q}是q0{displaystyle q_{0}}，動量p{displaystyle p}是p0{displaystyle p_{0}}。這些初始條件設定了這系統在時間t=0{displaystyle t=0}的狀態σ0{displaystyle sigma _{0}}。經典力學具有決定性，若知道粒子的初始條件與作用於粒子的外力，則可決定粒子的運動行為。

在實驗方面，製備經典系統在時間t=0{displaystyle t=0}的狀態σ0{displaystyle sigma _{0}}。稍後，在時間t>0{displaystyle t>0}，若想知道這系統的物理狀態σ(t){displaystyle sigma (t)}，可以測量這粒子的運動參數，即位置q(t){displaystyle q(t)}與動量p(t){displaystyle p(t)}。其它物理量，像加速度、動能等等，都是這兩個物理量的函數。

在理論方面，假設經典系統在t=0{displaystyle t=0}的狀態是σ0{displaystyle sigma _{0}}，則應用牛頓運動定律，即可計算出這系統在任何時間t>0{displaystyle t>0}的可觀察量數值。這些數值應該符合實驗測量的結果。標記這些數值為p(t){displaystyle p(t)}與q(t){displaystyle q(t)}。例如，假設粒子以等速移動，則

p(t)=p0{displaystyle p(t)=p_{0}}、

q(t)=p0t/m+q0{displaystyle q(t)=p_{0}t/m+q_{0}}；

其中，m{displaystyle m}是粒子質量。

量子力學的量子態

實驗的過程可以按照先後順序細分為製備與測量兩個步驟。在統計實驗（statistical experiment）裏，雖然以同樣的方法製備多個物理系統，然後以同樣的方法進行測量，仍舊不能可靠地獲得出同樣的結果，但是，假若經過很多次重複地製備與測量，則會發覺，同樣結果的出現頻率會收斂至某固定值。量子力學也具有類似特性，雖然每一次測量能夠很準確地獲得粒子運動地數據，但不能準確預測對於可觀察量做單次測量而獲得的結果，只能夠給出各種可能獲得的結果與獲得這結果的機率分佈，這是因為製備步驟必須遵守不確定性原理。^[4]:44-45

在量子系統裏，量子態可以從一系列製備程序來辨認，即這程序所製成的量子系統擁有這量子態。例如，使用z-軸方向的斯特恩-革拉赫實驗儀器，可以將入射的銀原子束，依照自旋的z-分量Sz{displaystyle S_{z}}分裂成兩道，一道的Sz{displaystyle S_{z}}為上旋，量子態為|↑⟩{displaystyle |uparrow rangle }或|z+⟩{displaystyle |z+rangle }，另一道的Sz{displaystyle S_{z}}為下旋，量子態為|↓⟩{displaystyle |downarrow rangle }或|z−⟩{displaystyle |z-rangle }。又例如，假若等待足夠長久時間，就可以使得量子系統衰變至基態，前提是從激發態只能朝著無窮遠發射出能量，永遠不會反射回來。這樣，就可以製備出基態。^[4]:206-209再照射適當頻率的激光，則可製備出指定的激發態。

在實驗方面，量子力學顯露出一種內稟統計行為。同樣的一個實驗重複地做很多次，每次實驗的測量結果通常不會一樣，只有從很多次的實驗結果計算出來的統計平均值，才是可複製的數值。假設，在每次實驗裏，在時間t=0{displaystyle t=0}，量子系統的量子態為|σ0⟩{displaystyle |sigma _{0}rangle }。稍後，在時間t>0{displaystyle t>0}，測量這粒子在各個量子系統的可觀察量q(t){displaystyle q(t)}或p(t){displaystyle p(t)}，則能獲得在時間t>0{displaystyle t>0}這些可觀察量的統計平均值。特別注意，對於這兩種可觀察量並不是一起進行測量，而是獨立分開進行測量。更詳細地說，重複地做很多次同樣的實驗，測量可觀察量q(t){displaystyle q(t)}。由於這可觀察量是隨機變量，所以無法可靠地複製同樣結果。但是，假若重複次數足夠多（概念而言，無窮多），則能獲得在時間t>0{displaystyle t>0}這可觀察量q(t){displaystyle q(t)}的統計平均值。類似地，重複地做很多次同樣的實驗，測量可觀察量p(t){displaystyle p(t)}，也能獲得在時間t>0{displaystyle t>0}這可觀察量p(t){displaystyle p(t)}的統計平均值。

在理論方面，假設量子系統在t=0{displaystyle t=0}的量子態是|σ0⟩{displaystyle |sigma _{0}rangle }，應用埃倫費斯特定理，可以計算出可觀察量在任何時間t>0{displaystyle t>0}的期望值。這期望值應該完全符合實驗獲得的統計平均值。標記這些期望值為⟨q(t)⟩{displaystyle langle q(t)rangle }、⟨p(t)⟩{displaystyle langle p(t)rangle }。假設沒有任何外力作用於自由移動的粒子，則

⟨p(t)⟩=⟨p(0)⟩{displaystyle langle p(t)rangle =langle p(0)rangle }、

⟨q(t)⟩=⟨p(0)⟩t/m+⟨q(0)⟩{displaystyle langle q(t)rangle =langle p(0)rangle t/m+langle q(0)rangle }。

位置的期望值與動量的期望值表現出類似經典力學的運動行為。在量子力學裏，量子態可以預測所有測量可觀察量的實驗統計結果。

薛丁格繪景與海森堡繪景

量子系統的每一種可觀察量都有其對應的量子算符。將這量子算符作用於量子態，可以詮釋為測量其量子系統的可觀察量。在前一節量子力學論述裏，量子算符q(t){displaystyle q(t)}，p(t){displaystyle p(t)}被設定為與時間有關，而量子態則在初始時間t=0{displaystyle t=0}就被固定為|σ0⟩{displaystyle |sigma _{0}rangle }，與時間無關。這種理論方法稱為海森堡繪景。另一種稱為薛丁格繪景的理論方法設定量子算符與時間無關，又設定量子態與時間有關。在概念方面或在數學方面，這兩種繪景等價，推導出的結果一樣。大多數初級量子力學教科書採用的是薛丁格繪景，通過生動活潑的量子態，學生可以迅速地瞭解量子系統如何隨著時間演變。海森堡繪景比較適用於研究一些像對稱性或守恆定律的基礎論題領域，例如量子場論，或者研究超大自由度系統的學術，例如統計力學。^[5]

量子力學形式論

主条目：量子力學的數學表述

量子物理通常使用線性代數來做數學表述。每一種量子系統都有其對應的希爾伯特空間，其量子態都可以用對應的希爾伯特空間裏的向量來表現，這向量稱為態向量。假若，某態向量是另外一個態向量的純量倍數，則這兩個態向量都對應於同樣的量子態。因此，態向量的範數不具有物理意義，只有方向具有物理意義。

假若將態向量歸一化，所有態向量的範數都等於1，則所有態向量的集合是希爾伯特空間的單位球。假若，兩個歸一化態向量的唯一不同之處是它們的相位因子，則這兩個態向量代表同樣的量子態。

狄拉克標記

主条目：狄拉克標記

在量子力學裏，數學運算時常用到線性算符、內積、對偶空間與厄米共軛等概念。為了讓運算更加簡易、更加抽象，為了讓使用者不需要選擇表現空間，保羅·狄拉克發明了狄拉克標記。這種標記法能夠精準地表示各種各樣的量子態與其相關運算，簡略表述如下：

• 向量的標記形式為|ψ⟩{displaystyle |psi rangle }；其中ψ{displaystyle psi }可以是任何符號，字母，數字，或單字。這與一般的數學標記形式顯然地不同；通常，向量是以粗體字母，或者在上方加了一個矢號的字母來標記。


• 稱向量為「右矢」。


• 對於每一個右矢|ψ⟩{displaystyle |psi rangle }，都獨特地存在一個對應的左矢⟨ψ|{displaystyle langle psi |}，左矢與右矢指的是同一個量子態。在數學裏，左矢與右矢分別是彼此的厄米共軛，左矢屬於另外一個希爾伯特空間，稱為對偶空間。假設右矢|ψ⟩{displaystyle |psi rangle }的維度為有限值，則可以將右矢寫為豎排，左矢寫為橫排；取右矢的厄米共軛（即取轉置運算加上共軛複數運算），就可以得到左矢。


• 左矢⟨ϕ|{displaystyle langle phi |}與右矢|ψ⟩{displaystyle |psi rangle }的內積，可以寫為⟨ϕ|ψ⟩{displaystyle langle phi |psi rangle }。這內積的物理意義為在量子態|ϕ⟩{displaystyle |phi rangle }裏找到量子態|ψ⟩{displaystyle |psi rangle }的機率幅。^[1]:50
  

量子態的測量

量子理論只能從量子態計算出可觀察量的機率分佈，因此只能預測可觀察量的機率分佈，除了一些特別案例之外，不能準確預測（機率小於1）對可觀察量做測量獲得的數值，這反映出經典物理與量子物理之間的重要差異，在經典力學裏，測量的結果本質上是決定性的，而不是機率性的。儘管如此，在量子力學裏，對於任意可觀察量，必定存在一組本徵態。假設量子系統的量子態是其中任意本徵態，則測量這量子系統的可觀察量得到的數值必定等於其對應的本徵值，量子力學可以準確預測這本徵值

反過來說，假設給定了量子系統所有可觀察量的機率分佈，則可決定量子系統的量子態。^[4]:46-47但是，決定量子態，並不一定需要所有可觀察量的機率分佈；大多數時候，只需要給定某些可觀察量的機率分佈，就可以決定量子態，其它可觀察量的機率分佈，可以從量子態計算出來。

假設，某量子系統的可觀察量標記為O{displaystyle O}，其對應的量子算符O^{displaystyle {hat {O}}}，可能有很多不同的本徵值Oi{displaystyle O_{i}}與對應的本徵態|ei⟩{displaystyle |e_{i}rangle }，這些本徵態|ei⟩,i=1, 2, 3, ⋯{displaystyle |e_{i}rangle ,quad i=1, 2, 3, cdots }，形成了具有正交歸一性的基底：^[2]:96-99

⟨ei|ej⟩=δij{displaystyle langle e_{i}|e_{j}rangle =delta _{ij}}；

其中，δij{displaystyle delta _{ij}}是克羅內克函數。

描述這量子系統的量子態|ψ⟩{displaystyle |psi rangle }，可以用這基底表示為

|ψ⟩=∑i ci|ei⟩{displaystyle |psi rangle =sum _{i} c_{i}|e_{i}rangle }；

其中，ci=⟨ei|ψ⟩{displaystyle c_{i}=langle e_{i}|psi rangle }是複係數，是在量子態|ei⟩{displaystyle |e_{i}rangle }裏找到量子態|ψ⟩{displaystyle |psi rangle }的機率幅。^[1]:50

重複地做很多次同樣的實驗，在每次實驗裏，量子系統的量子態都設定為|ψ⟩{displaystyle |psi rangle }，則對於每一個量子系統的可觀察量O{displaystyle O}做測量，可能得到的結果是各種本徵態|ei⟩{displaystyle |e_{i}rangle }的本徵值Oi{displaystyle O_{i}}，獲得這些不同結果的次數具有機率性，可以表達為機率分佈，結果為Oi{displaystyle O_{i}}的機率是|ci|2{displaystyle |c_{i}|^{2}}。

假設測量的結果是本徵值Oi{displaystyle O_{i}}，則可以推斷測量後的量子態是本徵態|ei⟩{displaystyle |e_{i}rangle }。假若立刻再測量可觀察量O{displaystyle O}，由於量子態仍舊是本徵態|ei⟩{displaystyle |e_{i}rangle }，所得到的測量值是本徵值Oi{displaystyle O_{i}}的機率為1，量子態|ψ⟩{displaystyle |psi rangle }是「確定態」。

設想另一種可觀察量R{displaystyle R}，其對應的算符R^{displaystyle {hat {R}}}與算符O^{displaystyle {hat {O}}}的對易關係為

[R^,O^]≠0{displaystyle [{hat {R}},{hat {O}}]neq 0}，

稱這兩種可觀察量為不相容可觀察量。假若立刻再對本徵態|ei⟩{displaystyle |e_{i}rangle }測量可觀察量R{displaystyle R}，則又會得到統計性的答案。

單粒子系統的基底量子態

離散案例

假設，某量子系統的可觀察量標記為O{displaystyle O}，其對應的量子算符O^{displaystyle {hat {O}}}，可能有很多不同的本徵值Oi{displaystyle O_{i}}與對應的本徵態|ei⟩{displaystyle |e_{i}rangle }，這些本徵態|ei⟩,i=1, 2, 3, ⋯{displaystyle |e_{i}rangle ,quad i=1, 2, 3, cdots }，形成了具有正交歸一性的基底。^[2]:96-99描述這量子系統的量子態|ψ⟩{displaystyle |psi rangle }，可以用這基底的本徵態表示為

|ψ⟩=∑i ci|ei⟩{displaystyle |psi rangle =sum _{i} c_{i}|e_{i}rangle }；

其中，ci=⟨ei|ψ⟩{displaystyle c_{i}=langle e_{i}|psi rangle }是複係數，是在量子態|ei⟩{displaystyle |e_{i}rangle }裏找到量子態|ψ⟩{displaystyle |psi rangle }的機率幅。^[1]:50

ci{displaystyle c_{i}}是|ψ⟩{displaystyle |psi rangle }與|ei⟩{displaystyle |{e_{i}}rangle }的內積：

ci=⟨ei|ψ⟩{displaystyle c_{i}=langle {e_{i}}|psi rangle }。

因此，|ψ⟩{displaystyle |psi rangle }可以表示為

|ψ⟩=∑i|ei⟩⟨ei|ψ⟩{displaystyle |psi rangle =sum _{i}|e_{i}rangle langle {e_{i}}|psi rangle }。

定義投影算符Λ^i{displaystyle {hat {Lambda }}_{i}}為

Λ^i =def |ei⟩⟨ei|{displaystyle {hat {Lambda }}_{i} {stackrel {def}{=}} |e_{i}rangle langle {e_{i}}|}。

投影算符Λ^i{displaystyle {hat {Lambda }}_{i}}作用於量子態，投射出平行於|ei⟩{displaystyle |{e_{i}}rangle }的部分：

Λ^i|ψ⟩=|ei⟩⟨ei|ψ⟩=ci|ei⟩{displaystyle {hat {Lambda }}_{i}|psi rangle =|{e_{i}}rangle langle {e_{i}}|psi rangle =c_{i}|{e_{i}}rangle }。

量子態|ψ⟩{displaystyle |psi rangle }是所有投影部分的總和：

|ψ⟩=∑i|ei⟩⟨ei|ψ⟩=∑iΛ^i|ψ⟩{displaystyle |psi rangle =sum _{i}|{e_{i}}rangle langle {e_{i}}|psi rangle =sum _{i}{hat {Lambda }}_{i}|psi rangle }；

由於量子態|ψ⟩{displaystyle |psi rangle }可以是任意量子態，因此，基底量子態具有閉包性，或完備性：

∑iΛ^i=∑i|ei⟩⟨ei|=1{displaystyle sum _{i}{hat {Lambda }}_{i}=sum _{i}|e_{i}rangle langle {e_{i}}|=1}；

其中，在公式最右邊的1{displaystyle 1}代表單位算符。

由於這基底滿足正交歸一性，

⟨ψ|ψ⟩=∑i|ci|2=1{displaystyle langle psi |psi rangle =sum _{i}|c_{i}|^{2}=1}。

連續案例

位置x{displaystyle x}是一種連續的可觀察量，具有連續的本徵值譜：

x^|x⟩=x|x⟩{displaystyle {hat {x}}|xrangle =x|xrangle }；

其中，x^{displaystyle {hat {x}}}是對應於可觀察量x{displaystyle x}的算符，|x⟩{displaystyle |xrangle }是本徵值為x{displaystyle x}的連續本徵態。

對於這連續本徵態|x⟩{displaystyle |xrangle }所組成的基底，必須將前一節提到的離散和，加以修改為積分：

|ψ⟩=∫−∞∞dx |x⟩⟨x|ψ⟩{displaystyle |psi rangle =int _{-infty }^{infty }mathrm {d} x |xrangle langle x|psi rangle }。

又必須將克羅內克函數改變為狄拉克δ函數：

⟨x|x′⟩=δ(x−x′){displaystyle langle x|x'rangle =delta (x-x')}。

由於量子態|ψ⟩{displaystyle |psi rangle }可以是任意量子態，因此，連續基底量子態具有閉包性，或完備性：

∫−∞∞dx |x⟩⟨x|=1{displaystyle int _{-infty }^{infty }mathrm {d} x |xrangle langle x|=1}。

由於這基底滿足正交歸一性，

⟨ψ|ψ⟩=∫−∞∞dx ⟨ψ|x′⟩⟨x′|x⟩⟨x|ψ⟩=∫−∞∞dx δ(x−x′)⟨ψ|x′⟩⟨x|ψ⟩=∫−∞∞dx |⟨x|ψ⟩|2=1{displaystyle langle psi |psi rangle =int _{-infty }^{infty }mathrm {d} x langle psi |x'rangle langle x'|xrangle langle x|psi rangle =int _{-infty }^{infty }mathrm {d} x delta (x-x')langle psi |x'rangle langle x|psi rangle =int _{-infty }^{infty }mathrm {d} x |langle x|psi rangle |^{2}=1}。

從這方程式，可以推論|⟨x|ψ⟩|2dx{displaystyle |langle x|psi rangle |^{2}mathrm {d} x}是粒子處於位置x{displaystyle x}與x+dx{displaystyle x+mathrm {d} x}之間的機率。

內積⟨x|ψ⟩{displaystyle langle x|psi rangle }就是波動力學的波函數ψ(x){displaystyle psi (x)}：

ψ(x) =def ⟨x|ψ⟩{displaystyle psi (x) {stackrel {def}{=}} langle x|psi rangle }。

態疊加原理

主条目：態疊加原理

雙縫實驗草圖，從光源a{displaystyle a}散發出來的單色光，照射在一座有兩條狹縫b{displaystyle b}與c{displaystyle c}的不透明擋牆S2{displaystyle S2}。在擋牆的後面，設立了一個照相底片或某種偵測屏障F{displaystyle F}，用來紀錄到達F{displaystyle F}的任何位置d{displaystyle d}的光波數據。最右邊黑白相間的條紋，顯示出光波在偵測屏障F{displaystyle F}的干涉圖樣

假設某量子系統的量子態可能是|α⟩{displaystyle |alpha rangle }或|β⟩{displaystyle |beta rangle }這兩個不同的歸一化量子態，則這量子系統也可能處於它們線性疊加而成的量子態cα|α⟩+cβ|β⟩{displaystyle c_{alpha }|alpha rangle +c_{beta }|beta rangle }（可能尚未歸一化）。假設θ{displaystyle theta }為實數，則雖然量子態eiθ|β⟩{displaystyle e^{itheta }|beta rangle }與|β⟩{displaystyle |beta rangle }對應於同樣的量子態，他們並無法互相替換。例如，|α⟩+|β⟩{displaystyle |alpha rangle +|beta rangle }和|α⟩+eiθ|β⟩{displaystyle |alpha rangle +e^{itheta }|beta rangle }是兩個不同的量子態。但是，|α⟩+|β⟩{displaystyle |alpha rangle +|beta rangle }和eiθ(|α⟩+|β⟩){displaystyle e^{itheta }(|alpha rangle +|beta rangle )}對應於同一個量子態。因此可以這樣說，整體的相位因子並不具有物理意義，但相對的相位因子具有重要的物理意義。

例如，在雙縫實驗裏，光子的量子態是兩個不同量子態的疊加。其中一個量子態是通過狹縫b{displaystyle b}。另外一個量子態是通過狹縫c{displaystyle c}。光子抵達偵測屏障的位置d{displaystyle d}，這位置離開兩條狹縫的距離之差值bd−cd{displaystyle bd-cd}，與兩個量子態的相對相位有關。由於這相對相位，在偵測屏障的某些位置，會造成相长干涉，在另外一些位置，會造成相消干涉。

再舉一個例子，拉比振動，可以顯示出相對相位在量子態疊加中的重要性。這是一個雙態系統，兩個本徵態的本徵能級不一樣。那麼，因為態疊加的相對相位隨著時間而改變，疊加後的量子態會反復不停地振動於兩個本徵態。

參閱

• 量子諧振子


• 定態


• 激發態

註釋

參考文獻

1. 
   ^ ^{1.01.11.21.31.4} Sakurai, J. J.; Napolitano, Jim, Modern Quantum Mechanics 2nd, Addison-Wesley, 2010, ISBN 978-0805382914 
   


2. 
   ^ ^2.02.12.2 Griffiths, David J., Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, 2004, ISBN 0-13-111892-7 
   


3. 
   ^ ^3.03.13.2 Laloe, Franck, Do We Really Understand Quantum Mechanics, Cambridge University Press, 2012, ISBN 978-1-107-02501-1 
   


4. 
   ^ ^4.04.14.2 Ballentine, Leslie. Quantum Mechanics: A Modern Development 2nd, illustrated, reprint. World Scientific. 1998. ISBN 9789810241056. 
   


5. 
   ^ Gottfried, Kurt; Yan, Tung-Mow. Quantum Mechanics: Fundamentals 2nd, illustrated. Springer. 2003: pp. 65. ISBN 9780387955766.  引文格式1维护：冗余文本 (link)
   

查 论 编 量子力学 入门 · 數學表述 · 歷史 基础 狄拉克符號 波函數 量子態 態向量 態疊加原理 不确定性原理 波粒二象性 互補原理 埃倫費斯特定理 泡利不相容原理 量子纠缠 量子退相干 量子穿隧效應 量子測量 爱波罗佯谬 贝尔不等式 密度矩阵 表述 數學表述 薛丁格繪景 海森堡繪景 相互作用繪景 矩陣力學 求和的歷史（路径积分） 相空间表述 方程 薛定谔方程 狄拉克方程式 克莱因-戈尔登方程 包立方程式 里德伯公式 詮釋 量子力學詮釋 哥本哈根詮釋 系綜詮釋 隱變量理論 客觀坍縮理論 德布罗意-玻姆理论 多世界詮釋 一致性歷史 關係性量子力學 交易詮釋 实验 阿弗沙爾實驗 貝爾定理的實驗驗證 波普爾實驗 戴維森－革末實驗 馬赫-曾德爾干涉儀 光电效应 量子擦除實驗 墨子号卫星 施特恩－格拉赫实验 雙縫實驗 薛定谔猫 伊利澤-威德曼炸彈 惠勒延迟选择实验 物理學者 普朗克 玻尔 埃倫費斯特 海森堡 薛丁格 德布羅意 玻恩 愛因斯坦 艾弗雷特 索末菲 馮·诺伊曼 費曼 狄拉克 泡利 維恩 阿哈罗诺夫 玻姆 貝爾 蔡林格 交叉領域 半經典物理學 量子生物学 量子化学 介觀物理學 量子宇宙學 量子群 量子时空（英语：Quantum spacetime） 量子光学 量子混沌（英语：Quantum chaos） 技术應用（英语：Quantum technology） 量子線路 量子复杂性理论 量子计算机 量子密碼學 量子閘 量子邏輯（英语：Quantum logic） 量子信息学 量子密鑰分發 量子网络 量子隱形傳態 進階研究 相对论量子力学 量子场论 量子引力 分类 Portal:物理学 维基共享

This page is only for reference, If you need detailed information, please check here