多方球





Confusion grey.svg  提示：本条目的主题不是多胞形。





在天文物理學上的多方球（或稱為多層球，Polytrope），是指莱恩－埃姆登方程中壓力與密度關係的解，表示方程式為 P=Kρ((n+1)/n){displaystyle P=Krho ^{((n+1)/n)}}{displaystyle P=Krho ^{((n+1)/n)}}。這裡 P{displaystyle P}P 是壓力、ρ{displaystyle rho }rho 是密度、K{displaystyle K}K 是常數、常數 n{displaystyle n}n 則是多方指數。這個關係式並不能解釋為状态方程，雖然遵循這個方程式狀態的氣體會在莱恩－埃姆登方程中有多個解。相反地，這是表示一個假設中壓力 P{displaystyle P}P 和半徑以及密度 ρ{displaystyle rho }rho 和半徑變化的簡單關係式，產生了莱恩－埃姆登方程的解。


有時候「Polytrope」可能會用來指一個看起來類似上述類似的熱力學關係狀態方程，雖然這可能造成混亂必須要避免。這個詞比較適合用來指流體本身（而不是莱恩－埃姆登方程的解）。多方流體的狀態方程使用相當廣泛，因此這樣的理想化流體可在多方球的限制性問題之外廣泛出現。



不同的多方指數下範例




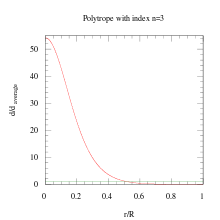
密度（歸一化平均密度）和半徑（歸一化到外部半徑）在多方指數是3的狀態下關係。



  • 中子星在 n=0.5{displaystyle n=0.5}{displaystyle n=0.5} 到 n=1{displaystyle n=1}n=1 之間時可良好擬合多方球概念模型。


  • n=1.5{displaystyle n=1.5}{displaystyle n=1.5} 的多方球擬合以简并态物质組成的恆星核心（例如紅巨星的核心）、白矮星、棕矮星、氣體巨行星，甚至是類地行星。

  • 太陽等主序星則符合 n=3{displaystyle n=3}n=3 時的模型，這對應恆星結構的愛丁頓標準模型。


  • n=5{displaystyle n=5}n=5 時半徑無限大。這對應最簡單的自洽恆星系統合理模型，該模型首次由阿瑟·舒斯特於1883年首次提出。

  • 如果 n=∞{displaystyle n=infty }{displaystyle n=infty }，這個狀況對應於「絕熱球」，這是絕熱的自重力氣體球，它的結構和球狀星團中無碰撞恆星系統的結構相同。

注意多方指數越高，在中心的密度分布就越緊密。



參考資料



  • Chandrasekhar, S. [ 1939 ] ( 1958 ). An Introduction to the Study of Stellar Structure, New York : Dover. ISBN 0-486-60413-6

  • Hansen, C.J., Kawaler S.D. & Trimble V. ( 2004 ). Stellar Interiors - Physical Principles, Structure, and Evolution, New York : Springer. ISBN 0-387-20089-4

  • Horedt, G.P. ( 2004 ). Polytropes. Applications in Astrophysics and Related Fields, Dordrecht : Kluwer. ISBN 1-4020-2350-2










Comments

Post a Comment

Popular posts from this blog

Information security

Image
This article is part of a series on Information security Related security categories Internet security Cyberwarfare Computer security Mobile security Network security Threats Computer crime Vulnerability Eavesdropping Malware Spyware Ransomware Trojans Viruses Worms Rootkits Bootkits Keyloggers Screen scrapers Exploits Backdoors Logic bombs Payloads Denial of service Defenses Computer access control Application security Antivirus software Secure coding Secure by default Secure by design Secure operating systems Authentication Multi-factor authentication Authorization Data-centric security Encryption Firewall Intrusion detection system Mobile secure gateway Runtime application self-protection (RASP) v t e Information security , sometimes shortened to InfoSec , is the practice of preventing unauthorized access, use, disclosure, disruption, modification, inspection, recording or destruction of information. Th...
Read more

Lambak Kiri

Image
For Lambak Kiri public housing area, see Lambak Kiri Landless Indigenous Citizens' Housing Scheme. Village in Brunei-Muara, Brunei Lambak Kiri Village Location in Brunei Coordinates: 4°59′26″N 114°57′04″E  /  4.990472°N 114.951114°E  / 4.990472; 114.951114 Coordinates: 4°59′26″N 114°57′04″E  /  4.990472°N 114.951114°E  / 4.990472; 114.951114 Country Brunei District Brunei-Muara Mukim Berakas A Government  • Village head Hamdani Omar Postcode BB1214 Lambak Kiri is a populated place in Brunei-Muara District, Brunei. It is officially a village subdivision under Berakas A, a mukim in the district. Lambak Kiri may also refer to the greater area which includes the Lambak Kiri public housing area of the Landless Indigenous Citizens' Housing Scheme (Malay: Skim Tanah Kurnia Rakyat Jati ), although the latter is a separate subdivision. Contents 1 Name 2 Administration 3 See also 4 References Name ...
Read more

章鱼与海女图

Image
本条目 可参照英語維基百科相應條目来扩充 。 （2014/5/25） 若您熟悉来源语言和主题，请协助参考外语维基扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记 {{Translated page}} 标签。 本条目 需要擴充。 （2013年8月15日） 请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 《 章鱼与海女 》（日语： 蛸と海女 ／ たことあま   Tako to ama ）是一幅由日本畫家葛饰北斋创作的浮世绘，出自1814年（文化4年）出版的艳本《喜能会之故真通》（日语： 喜能会之故真通 ／ きのえのこまつ   Kinoe no Komatsu ）。畫中有兩隻章鱼以觸手攻擊一名採珠的海女，並進行擬似戀獸癖的交媾行為。作品尺寸为6½" × 8¾" （16.51 cm × 22.23 cm）。 [1] 在此之前的类似作品还有北尾重政的艳本《謡曲色番組》及勝川春潮的艳本《艳本千夜多女志》等，有被北斋作为参考的可能性。 《章鱼与海女图》有不同英文翻译，一般称The Dream of the Fisherman's Wife，又作Girl Diver and Octopi、Diver and Two Octopi，Richard Douglas Lane称其为 Girl Diver and Octopi [2] ，Mathi Forrer 称其为 Pearl Diver and Two Octopi [3] ，Danielle Talerico 称其为 Diver and Two Octopi 。 [4] 目录 1 作品介绍 1.1 画中对话 1.2 解释 2 评价 3 影响 3.1 模仿作品 4 另见 5 参考来源 6 外部連結 作品介绍 画中对话 原文 译文 大蛸： いつぞハいつぞハとねらいすましてゐたかいがあつて、けふといふけふ、とうとうとらまへたア。てもむつくりとしたいいぼぼだ。いもよりハなをこうぶつだ。サアサア、すつてすつてすいつくして...
Read more