朗伯W函数

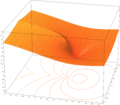
W₀(x)的图像，−1/e ≤ x ≤ 4

朗伯W函数（英语：Lambert W function，又称为欧米加函数或乘积对数），是f(w) = we^w的反函数，其中e^w是指数函数，w是任意复数。对于任何复数z，都有：

z=W(z)eW(z).{displaystyle z=W(z)e^{W(z)}.}

由于函数f不是单射，因此函数W是多值的（除了0以外）。如果我们把x限制为实数，并要求w是实数，那么函数仅对于x ≥ −1/e有定义，在(−1/e, 0)内是多值的；如果加上w ≥ −1的限制，则定义了一个单值函数W₀(x)（见图）。我们有W₀(0) = 0，W₀(−1/e) = −1。而在[−1/e, 0)内的w ≤ −1分支，则记为W₋₁(x)，从W₋₁(−1/e) = −1递减为W₋₁(0⁻) = −∞。

朗伯W函数不能用初等函数来表示。它在组合数学中有许多用途，例如树的计算。它可以用来解许多含有指数的方程，也出现在某些微分方程的解中，例如y'(t) = a y(t − 1)。

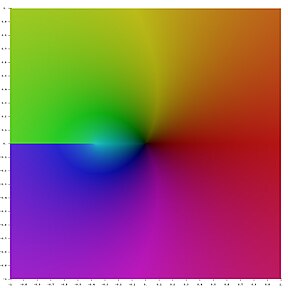
复平面上的朗伯W函数

目录

• 
  1 微分和积分
  


• 
  2 性质
  


• 
  3 泰勒级数
  


• 
  4 加法定理
  


• 
  5 複數值
  


• 
  6 特殊值
  


• 
  7 应用
  
  
  
  • 
    7.1 例子
    
  
  
  
  


• 
  8 一般化
  


• 
  9 图象
  


• 
  10 计算
  


• 
  11 参考来源
  


• 
  12 外部链接
  

微分和积分

朗伯 W{displaystyle W,}函数的积分形式为

W(x)=xπ∫0π(1−vcot⁡v)2+v2x+vcsc⁡v⋅e−vcot⁡vdv,|arg⁡(x)|<π{displaystyle W(x)={frac {x}{pi }}int _{0}^{pi }{frac {left(1-vcot vright)^{2}+v^{2}}{x+vcsc vcdot e^{-vcot v}}}{rm {d}}v,|arg left(xright)|<pi ,}

W(x)=∫−∞−1e−1πℑ[ddxW(x)]ln⁡(1−zx)dx{displaystyle W(x)=int _{-infty }^{-{frac {1}{e}}}{-{frac {1}{pi }}}Im left[{frac {rm {d}}{{rm {d}}x}}W(x)right]ln left(1-{frac {z}{x}}right){rm {d}}x,}

若 x∉[−1e,0],k∈Z{displaystyle xnot in left[-{frac {1}{e}},0right],kin {mathbb {Z} },} ,若 x∈(−1e,0),k=1,±2,±3,...{displaystyle xin left(-{frac {1}{e}},0right),k=1,pm 2,pm 3,...,}

Wk(x)=1+(ln⁡x−1+2kπi)ei2π∫0∞ln⁡t−ln⁡t+ln⁡x+(2k+1)πit−ln⁡t+ln⁡x+(2k−1)πi⋅dtt+1=1+(ln⁡x−1+2kπi)ei2π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(4k2−1)π2+2π(t−ln⁡t+ln⁡x)i(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1{displaystyle W_{k}(x)=1+left(ln x-1+2kpi {rm {i}}right)e^{{frac {rm {i}}{2pi }}int _{0}^{infty }ln {frac {t-ln t+ln x+(2k+1)pi {rm {i}}}{t-ln t+ln x+(2k-1)pi {rm {i}}}}cdot {frac {{rm {d}}t}{t+1}}}=1+left(ln x-1+2kpi {rm {i}}right)e^{{frac {rm {i}}{2pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}+2pi left(t-ln t+ln xright){rm {i}}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}},}

把被积函数的实部和虚部分离出来：

Wk(x)=1+(ln⁡x−1+2kπi)ei2π∫0∞[12ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2+iarctan⁡2π(t−ln⁡t+ln⁡x)(t−ln⁡t+ln⁡x)2+(4k2−1)π2]⋅dtt+1{displaystyle W_{k}(x)=1+left(ln x-1+2kpi {rm {i}}right)e^{{frac {rm {i}}{2pi }}int _{0}^{infty }left[{frac {1}{2}}ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}+{rm {i}}arctan {frac {2pi left(t-ln t+ln xright)}{left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}}}right]cdot {frac {{rm {d}}t}{t+1}}}}

Wk(x)=1+(ln⁡x−1)cos⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1−2kπsin⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1+i[(ln⁡x−1)sin⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1+2kπcos⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1]e12π∫0∞arctan⁡2π(t−ln⁡t+ln⁡x)(t−ln⁡t+ln⁡x)2+(4k2−1)π2⋅dtt+1{displaystyle {}_{W_{k}(x)=1+{frac {left(ln x-1right)cos {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}-2kpi sin {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}+{rm {i}}left[left(ln x-1right)sin {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}+2kpi cos {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}right]}{e^{{frac {1}{2pi }}int _{0}^{infty }arctan {frac {2pi left(t-ln t+ln xright)}{left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}}}cdot {frac {rm {{d}t}}{t+1}}}}}}}

设 Wk(x)=u+vi,x=t+si{displaystyle W_{k}(x)=u+v{rm {i}},x=t+s{rm {i}}} ，则有 (u+vi)eu+vi=t+si{displaystyle left(u+v{rm {i}}right)e^{u+v{rm {i}}}=t+s{rm {i}}} ，展开分离出实部和虚部，

eu(ucos⁡v−vsin⁡v)=t,eu(usin⁡v+vcos⁡v)=s{displaystyle e^{u}left(ucos v-vsin vright)=t,e^{u}left(usin v+vcos vright)=s},当s=0{displaystyle s=0}时，易知 u=−vcot⁡v{displaystyle u=-vcot v}

Wk(x)=(1−ln⁡x)sin⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1−2kπcos⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1e12π∫0∞arctan⁡2π(t−ln⁡t+ln⁡x)(t−ln⁡t+ln⁡x)2+(4k2−1)π2⋅dtt+1cot⁡(ln⁡x−1)sin⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1+2kπcos⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1e12π∫0∞arctan⁡2π(t−ln⁡t+ln⁡x)(t−ln⁡t+ln⁡x)2+(4k2−1)π2⋅dtt+1+(ln⁡x−1)sin⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1+2kπcos⁡14π∫0∞ln⁡(t−ln⁡t+ln⁡x)2+(2k+1)2π2(t−ln⁡t+ln⁡x)2+(2k−1)2π2⋅dtt+1e12π∫0∞arctan⁡2π(t−ln⁡t+ln⁡x)(t−ln⁡t+ln⁡x)2+(4k2−1)π2⋅dtt+1i,{displaystyle {}_{W_{k}(x)={frac {left(1-ln xright)sin {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}-2kpi cos {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}}{e^{{frac {1}{2pi }}int _{0}^{infty }arctan {frac {2pi left(t-ln t+ln xright)}{left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}}}cdot {frac {rm {{d}t}}{t+1}}}}}cot {frac {left(ln x-1right)sin {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}+2kpi cos {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}}{e^{{frac {1}{2pi }}int _{0}^{infty }arctan {frac {2pi left(t-ln t+ln xright)}{left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}}}cdot {frac {rm {{d}t}}{t+1}}}}}+{frac {left(ln x-1right)sin {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}+2kpi cos {frac {1}{4pi }}int _{0}^{infty }ln {frac {left(t-ln t+ln xright)^{2}+left(2k+1right)^{2}pi ^{2}}{left(t-ln t+ln xright)^{2}+left(2k-1right)^{2}pi ^{2}}}cdot {frac {{rm {d}}t}{t+1}}}{e^{{frac {1}{2pi }}int _{0}^{infty }arctan {frac {2pi left(t-ln t+ln xright)}{left(t-ln t+ln xright)^{2}+left(4k^{2}-1right)pi ^{2}}}cdot {frac {rm {{d}t}}{t+1}}}}}{rm {i}},}}

W0(x)=1+(ln⁡x−1)e−1π∫0∞arg⁡(t−ln⁡t+ln⁡x+πi)⋅dtt+1,x>0{displaystyle W_{0}(x)=1+left(ln x-1right)e^{-{frac {1}{pi }}int _{0}^{infty }arg left(t-ln t+ln x+pi {rm {i}}right)cdot {frac {rm {{d}t}}{t+1}}},x>0}

若 x>1e{displaystyle x>{frac {1}{e}}} ，上式还可化为W0(x)=1+(ln⁡x−1)e−1π∫0∞arctan⁡πt−ln⁡t+ln⁡x⋅dtt+1{displaystyle W_{0}(x)=1+left(ln x-1right)e^{-{frac {1}{pi }}int _{0}^{infty }arctan {frac {pi }{t-ln t+ln x}}cdot {frac {rm {{d}t}}{t+1}}}}

由隐函数的求导法则，朗伯W{displaystyle W,}函数满足以下的微分方程：

z[1+W(z)]ddzW(z)=W(z){displaystyle zleft[1+W(z)right]{frac {rm {d}}{{rm {d}}z}}W(z)=W(z)}，z≠−1e,{displaystyle zneq -{frac {1}{e}},,}

因此：

ddzW(z)=W(z)z[1+W(z)]{displaystyle {frac {rm {d}}{{rm {d}}z}}W(z)={frac {W(z)}{zleft[1+W(z)right]}}}，z≠−1e.{displaystyle zneq -{frac {1}{e}},.}

函数W(x){displaystyle W(x),}，以及许多含有W(x){displaystyle W(x),}的表达式，都可以用w=W(x){displaystyle w=W(x),}的变量代换来积分，也就是说x=wew{displaystyle x=we^{w},}

∫W(x)dx=x[W(x)+1W(x)−1]+C{displaystyle int W(x){rm {d}}x=xleft[W(x)+{frac {1}{W(x)}}-1right]+C}

∫01W(x)dx=Ω+1Ω−2≈0.330366{displaystyle int _{0}^{1}W(x){rm {d}}x=Omega +{frac {1}{Omega }}-2approx 0.330366}

其中Ω{displaystyle Omega }為欧米加常数。

性质

1{displaystyle 1,}、zzzzz...=limn→∞(z⇈n)=−W(−ln⁡z)ln⁡z{displaystyle z^{z^{z^{z^{z^{.^{.^{.}}}}}}}=lim _{nto infty }(zupuparrows n)=-{frac {W(-ln z)}{ln z}}}，

其中⇈{displaystyle upuparrows }是高德納箭號表示法。

2{displaystyle 2,}、若z>0{displaystyle z>0,}，则ln⁡W(z)=ln⁡z−W(z){displaystyle ln W(z)=ln z-W(z),}

泰勒级数

W0{displaystyle W_{0},}在x=0{displaystyle x=0,}的泰勒级数如下：

W0(x)=∑n=1∞(−n)n−1n! xn=x−x2+32x3−83x4+12524x5−⋯{displaystyle W_{0}(x)=sum _{n=1}^{infty }{frac {(-n)^{n-1}}{n!}} x^{n}=x-x^{2}+{frac {3}{2}}x^{3}-{frac {8}{3}}x^{4}+{frac {125}{24}}x^{5}-cdots }

收敛半径为 1e{displaystyle {frac {1}{e}},} 。

加法定理

W(x)+W(y)=W[xyW(x)+xyW(y)]{displaystyle W(x)+W(y)=Wleft[{frac {xy}{W(x)}}+{frac {xy}{W(y)}}right],}

x>0,y>0{displaystyle x>0,y>0,}

複數值

實部

ℜ[W(x+yi)]=∑k=1∞(−k)k−1k!(x2+y2)kcos⁡(karctan⁡xy){displaystyle Re left[W(x+y{rm {i}})right]=sum _{k=1}^{infty }{frac {(-k)^{k-1}}{k!}}{sqrt {(x^{2}+y^{2})^{k}}}cos left(karctan {frac {x}{y}}right),} , x2+y2<1e2{displaystyle x^{2}+y^{2}<{frac {1}{e^{2}}},}

虛部

ℑ[W(x+yi)]=∑k=1∞(−k)k−1k!(x2+y2)ksin⁡(karctan⁡xy){displaystyle Im left[W(x+y{rm {i}})right]=sum _{k=1}^{infty }{frac {(-k)^{k-1}}{k!}}{sqrt {(x^{2}+y^{2})^{k}}}sin left(karctan {frac {x}{y}}right),}, x2+y2<1e2{displaystyle x^{2}+y^{2}<{frac {1}{e^{2}}},}

模長

|W(x+yi)|=W(x+y){displaystyle |W(x+y{rm {i}})|=W({sqrt {x+y}}),}

模角

arg⁡[W(x+yi)]=∑k=1∞(−k)k−1k!arctan⁡[cot⁡(karctan⁡xy)]{displaystyle arg left[W(x+y{rm {i}})right]=sum _{k=1}^{infty }{frac {(-k)^{k-1}}{k!}}arctan left[cot(karctan {frac {x}{y}})right],}, x2+y2<1e2{displaystyle x^{2}+y^{2}<{frac {1}{e^{2}}},}

共軛值

W(x+yi)¯=∑k=1∞(−k)k−1k!(x2+y2)k[cos⁡(karctan⁡xy)−isin⁡(karctan⁡xy)]{displaystyle {overline {W(x+y{rm {i}})}}=sum _{k=1}^{infty }{frac {(-k)^{k-1}}{k!}}{sqrt {(x^{2}+y^{2})^{k}}}left[cos left(karctan {frac {x}{y}}right)-{rm {i}}sin left(karctan {frac {x}{y}}right)right],}, x2+y2<1e2{displaystyle x^{2}+y^{2}<{frac {1}{e^{2}}},}

特殊值

W(−π2)=π2i{displaystyle Wleft(-{frac {pi }{2}}right)={frac {pi }{2}}i}

W(−ln⁡22)=−ln⁡2{displaystyle Wleft(-{frac {ln 2}{2}}right)=-ln 2}

W(−1e)=−1{displaystyle Wleft(-{1 over e}right)=-1}

W(1)=Ω=1∫−∞∞dx(ex−x)2+π2−1≈0.56714329…{displaystyle Wleft(1right)=Omega ={frac {1}{int _{-infty }^{infty }{frac {{rm {d}}x}{(e^{x}-x)^{2}+pi ^{2}}}}}-1approx 0.56714329dots ,}（欧米加常数）

W(e)=1{displaystyle W(e)=1,}

W(ee+1)=e{displaystyle W(e^{e+1})=e,}

W(1e1−1e)=1e{displaystyle Wleft({frac {1}{e^{1-{frac {1}{e}}}}}right)={frac {1}{e}}}

W(−1e)=−1{displaystyle W(-{frac {1}{e}})=-1}

W(πeπ)=π{displaystyle W({pi }e^{pi })=pi }

W(kln⁡k)=ln⁡k{displaystyle W(k{ln k})={ln k}} (k>0{displaystyle (k>0}

W(iπ)=−iπ{displaystyle W({rm {i}}pi )=-{rm {i}}pi }

W(−iπ)=iπ{displaystyle W(-{rm {i}}pi )={rm {i}}pi }

W(icos⁡1−sin⁡1)=i{displaystyle W({rm {i}}cos 1-sin 1)={rm {i}}}

W(−32π)=−32πi{displaystyle W(-{frac {3}{2}}{pi })=-{frac {3}{2}}{pi }{rm {i}}}

W(−877ln⁡2)=−327ln⁡2{displaystyle W(-{frac {sqrt[{7}]{8}}{7}}{ln 2})=-{frac {32}{7}}{ln 2}}

W(−354ln⁡3)=−92ln⁡3{displaystyle W(-{frac {sqrt {3}}{54}}{ln 3})=-{frac {9}{2}}{ln 3}}

W(−ln⁡24)=−4ln⁡2{displaystyle W(-{frac {ln 2}{4}})=-4{ln 2}}

W(−1)=e12π∫0∞1t+1arctan⁡2πt−ln⁡tdt−cos⁡[14π∫0∞1t+1ln⁡(t−ln⁡t)24π2+(t−ln⁡t)2dt]+πsin⁡[14π∫0∞1t+1ln⁡(t−ln⁡t)24π2+(t−ln⁡t)2dt]−i{πcos⁡[14π∫0∞1t+1ln⁡(t−ln⁡t)24π2+(t−ln⁡t)2dt]+sin⁡[14π∫0∞1t+1ln⁡(t−ln⁡t)24π2+(t−ln⁡t)2dt]}e12π∫0∞1t+1arctan⁡2πt−ln⁡tdt≈−0.31813−1.33723i{displaystyle Wleft(-1right)={frac {e^{{frac {1}{2pi }}int _{0}^{infty }{1 over t+1}arctan {2pi over t-ln t}{rm {d}}t}-cos left[{frac {1}{4pi }}int _{0}^{infty }{1 over t+1}ln {left(t-ln tright)^{2} over 4pi ^{2}+left(t-ln tright)^{2}}{rm {d}}tright]+pi sin left[{frac {1}{4pi }}int _{0}^{infty }{1 over t+1}ln {left(t-ln tright)^{2} over 4pi ^{2}+left(t-ln tright)^{2}}{rm {d}}tright]-{rm {i}}left{pi cos left[{frac {1}{4pi }}int _{0}^{infty }{1 over t+1}ln {left(t-ln tright)^{2} over 4pi ^{2}+left(t-ln tright)^{2}}{rm {d}}tright]+sin left[{frac {1}{4pi }}int _{0}^{infty }{1 over t+1}ln {left(t-ln tright)^{2} over 4pi ^{2}+left(t-ln tright)^{2}}{rm {d}}tright]right}}{e^{{frac {1}{2pi }}int _{0}^{infty }{1 over t+1}arctan {2pi over t-ln t}{rm {d}}t}}}approx -0.31813-1.33723{rm {i}}}

W(−ln⁡kk)=−ln⁡k{displaystyle W(-{frac {ln k}{k}})=-ln k}

W[−ln⁡(x+1)x(x+1)1x]=−x+1xln⁡(x+1)>,−1<x<0{displaystyle Wleft[-{frac {ln(x+1)}{x(x+1)^{frac {1}{x}}}}right]=-{frac {x+1}{x}}ln(x+1)>,-1<x<0}

应用

许多含有指数的方程都可以用W{displaystyle W,}函数来解出。一般的方法是把未知数都移到方程的一侧，并设法化为Y=XeX{displaystyle Y=Xe^{X},}的形式。

例子

例子1

2t=5t{displaystyle 2^{t}=5t,}

⇒1=5t2t{displaystyle Rightarrow 1={frac {5t}{2^{t}}},}

⇒1=5te−tln⁡2{displaystyle Rightarrow 1=5t,e^{-tln 2},}

⇒15=te−tln⁡2{displaystyle Rightarrow {frac {1}{5}}=t,e^{-tln 2},}

⇒−ln⁡25=(−tln⁡2)e−tln⁡2{displaystyle Rightarrow -{frac {ln 2}{5}}=(-,t,ln 2),e^{-tln 2},}

⇒−tln⁡2=Wk(−ln⁡25){displaystyle Rightarrow -tln 2=W_{k}left(-{frac {ln 2}{5}}right),}

⇒t=−Wk(−ln⁡25)ln⁡2{displaystyle Rightarrow t=-{frac {W_{k}left(-{frac {ln 2}{5}}right)}{ln 2}},}

更一般地，以下的方程

Qax+b=cx+d{displaystyle Q^{ax+b}=cx+d,}

其中

Q>0∧Q≠1∧c≠0{displaystyle Q>0land Qneq 1land cneq 0}

两边同乘: ac{displaystyle {frac {a}{c}}}，

得到：acQax+b=ax+adc{displaystyle {frac {a}{c}}Q^{ax+b}=ax+{frac {ad}{c}},}

同除以：Qax{displaystyle Q^{ax},}，

得到：acQb=(ax+adc)Q−ax{displaystyle {frac {a}{c}}Q^{b}=left(ax+{frac {ad}{c}}right)Q^{-ax},}

同除：Qadc{displaystyle Q^{frac {ad}{c}},}，

acQb−adc=(ax+adc)Q−(ax+adc){displaystyle {frac {a}{c}}Q^{b-{frac {ad}{c}}}=left(ax+{frac {ad}{c}}right)Q^{-left(ax+{frac {ad}{c}}right)},}

可以用变量代换

令t=ax+adc{displaystyle t=ax+{frac {ad}{c}}}

化为

tQ−t=acQb−adc{displaystyle tQ^{-t}={frac {a}{c}}Q^{b-{frac {ad}{c}}}}

即：t(eln⁡Q)−t=acQb−adc{displaystyle tleft(e^{ln Q}right)^{-t}={frac {a}{c}}Q^{b-{frac {ad}{c}}}}

同乘：ln⁡Q{displaystyle {ln Q},}

得出

tln⁡Q⋅e−tln⁡Q=ln⁡Q⋅acQb−adc{displaystyle t{ln Q}cdot e^{-tln Q}={ln Q}cdot {frac {a}{c}}Q^{b-{frac {ad}{c}}}}

故tln⁡Q=−Wk(−aln⁡QcQb−adc){displaystyle t{ln Q}=-W_{k}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}

带入t=ax+adc{displaystyle t=ax+{frac {ad}{c}}}

为

(ax+adc)ln⁡Q=−Wk(−aln⁡QcQb−adc){displaystyle left(ax+{frac {ad}{c}}right){ln Q}=-W_{k}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}

因此最终的解为

x=−Wk(−aln⁡QcQb−adc)aln⁡Q−dc{displaystyle x=-{frac {W_{k}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}{aln Q}}-{frac {d}{c}}}

若辅助方程：xex=−aln⁡QcQb−adc{displaystyle xe^{x}=-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}}中，

−aln⁡QcQb−adc∈(−∞,−1e){displaystyle -{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}in left(-infty ,-{frac {1}{e}}right)},

辅助方程无实数解，原方程亦无实解；

若：−aln⁡QcQb−adc∈{−1e}∪[0,+∞){displaystyle -{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}in left{-{frac {1}{e}}right}cup mathbf {[} 0,+infty )},

辅助方程有一实数解，原方程有一实解：

x=−Wk(−aln⁡QcQb−adc)aln⁡Q−dc{displaystyle x=-{frac {W_{k}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}{aln Q}}-{frac {d}{c}}}

若: −aln⁡QcQb−adc∈(−1e,0){displaystyle -{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}in left(-{frac {1}{e}},0right)},

辅助方程有二实解，设为W(−aln⁡QcQb−adc){displaystyle Wleft(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}，

W−1(−aln⁡QcQb−adc){displaystyle {rm {W}}_{-1}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}，

为

x1=−W(−aln⁡QcQb−adc)aln⁡Q−dc{displaystyle x_{1}=-{frac {Wleft(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}{aln Q}}-{frac {d}{c}}}

x2=−W−1(−aln⁡QcQb−adc)aln⁡Q−dc{displaystyle x_{2}=-{frac {{rm {W}}_{-1}left(-{frac {aln Q}{c}},Q^{b-{frac {ad}{c}}}right)}{aln Q}}-{frac {d}{c}}}

例子2

用类似的方法，可知以下方程的解

xx=t,{displaystyle x^{x}={mathrm {t} },,}

为

x=ln⁡tW(ln⁡t){displaystyle x={frac {ln {rm {t}}}{W(ln {rm {t}})}},}

或

x=exp⁡(Wk[ln⁡(t)]).{displaystyle x=exp left(W_{k}left[ln({rm {t}})right]right).}

例子3

以下方程的解

xlogb⁡x=a{displaystyle xlog _{b}{x}=a,}

具有形式

x=aln⁡bWk(aln⁡b){displaystyle x={frac {a{ln b}}{W_{k}left(a{ln b}right)}}}

例子4

xa−bx=0{displaystyle x^{a}-b^{x}=0,}

a>0{displaystyle a>0,} : b>0{displaystyle b>0,} : x>0{displaystyle x>0,}

取对数，

aln⁡x=xln⁡b{displaystyle aln x=xln b,}

ln⁡xx=ln⁡ba{displaystyle {frac {ln x}{x}}={frac {ln b}{a}},}

eln⁡xx=eln⁡ba{displaystyle e^{frac {ln x}{x}}=e^{frac {ln b}{a}},}

x1x=b1a{displaystyle x^{frac {1}{x}}=b^{frac {1}{a}},}

取倒数，

(1x)1x=b−1a{displaystyle left({frac {1}{x}}right)^{frac {1}{x}}=b^{-{frac {1}{a}}},}

1x=−ln⁡baW(−1aln⁡b){displaystyle {frac {1}{x}}=-{frac {ln b}{aWleft(-{frac {1}{a}}ln bright)}},}

最终解为 : x=−aln⁡bWk(−ln⁡ba){displaystyle x=-{frac {a}{ln b}}W_{k}left(-{frac {ln b}{a}}right),}

例子5

(ax+b)n=ucx+d{displaystyle (ax+b)^{n}=u^{cx+d},}

两边开n{displaystyle n,}次方并除以a{displaystyle a,}得

x+ba=ucnx+dna(cos⁡2kπn+isin⁡2kπn){displaystyle x+{frac {b}{a}}={frac {u^{{frac {c}{n}}x+{frac {d}{n}}}}{a}}left(cos {frac {2kpi }{n}}+{rm {i}}sin {frac {2kpi }{n}}right),}

令u=eln⁡u{displaystyle u=e^{ln u},} ，

化为

x+ba=ecln⁡unx+dln⁡una(cos⁡2kπn+isin⁡2kπn){displaystyle x+{frac {b}{a}}={frac {e^{{frac {cln u}{n}}x+{frac {dln u}{n}}}}{a}}left(cos {frac {2kpi }{n}}+{rm {i}}sin {frac {2kpi }{n}}right),}

两边同乘

−cln⁡unu−cnx−cbna{displaystyle -{frac {cln u}{n}}u^{-{frac {c}{n}}x-{frac {cb}{na}}},} ，

(−cln⁡unx−cbln⁡una)e−cln⁡unx−cbln⁡una=−cln⁡unaudn−cbna(cos⁡2kπn+isin⁡2kπn){displaystyle left(-{frac {cln u}{n}}x-{frac {cbln u}{na}}right)e^{-{frac {cln u}{n}}x-{frac {cbln u}{na}}}=-{frac {cln u}{na}}u^{{frac {d}{n}}-{frac {cb}{na}}}left(cos {frac {2kpi }{n}}+{rm {i}}sin {frac {2kpi }{n}}right),}

最终得

xk=−ncln⁡uWk[−cln⁡unaudn−cbna(cos⁡2kπn+isin⁡2kπn)]−ba{displaystyle x_{k}=-{frac {n}{cln u}}W_{k}left[-{frac {cln u}{na}}u^{{frac {d}{n}}-{frac {cb}{na}}}left(cos {frac {2kpi }{n}}+{rm {i}}sin {frac {2kpi }{n}}right)right]-{frac {b}{a}},}

k∈Z{displaystyle kin {mathbb {Z} },}

一般化

標準的 Lambert W 函數可用來表示以下超越代數方程式的解：

e−cx=ao(x−r)  (1){displaystyle e^{-cx}=a_{o}(x-r)~~quad qquad qquad qquad qquad (1)}

其中 a₀, c 與 r 為實常數。

其解為x=r+W(ce−crao)c{textstyle x=r+{tfrac {Wleft({frac {ce^{-cr}}{a_{o}}}right)}{c}}}

Lambert W 函數之一般化^[1][2][3] 包括:

• 一項在低維空間內廣義相對論與量子力學的應用（量子引力），實際上一種以前未知的 連結 於此二區域中，如 “Journal of Classical and Quantum Gravity”^[4] 所示其 (1) 的右邊式現為二維多項式 x：

e−cx=ao(x−r1)(x−r2)  (2){displaystyle e^{-cx}=a_{o}(x-r_{1})(x-r_{2})~~qquad qquad (2)}

其中 r₁ 和 r₂ 是不同實常數，為二維多項式的根。於此函數解有單一引數 x 但 r_i 和 a_o 為函數的參數。如此一來，此一般式類似於 “hypergeometric”（超几何分布）函數與 “Meijer G“，但屬於不同類函數。當 r₁ = r₂，(2)的兩方可分解為 (1) 因此其解簡化為標準 W 函數。(2)式代表著 “dilaton”（軸子）場的方程，可據此推導線性，雙體重力問題 1+1 維（一空間維與一時間維）當兩不等（靜止）質量，以及，量子力學的特徵能Delta位勢阱給不等電位於一維空間。

• 量子力學的一特例特徵能的分析解三體問題，亦即（三維）氢分子離子。^[5]於此 (1)（或 (2)）的右手邊現為無限級數多項式之比於 x：

e−cx=ao∏i=1∞(x−ri)∏i=1∞(x−si)(3){displaystyle e^{-cx}=a_{o}{frac {prod _{i=1}^{infty }(x-r_{i})}{prod _{i=1}^{infty }(x-s_{i})}}qquad qquad qquad (3)}

其中 r_i 與 s_i 是相異實常數而 x 是特徵能和內核距離R之函數。式 (3) 與其特例表示於 (1) 和 (2) 是與一更大類型延遲微分方程。由于哈代的“虚假导数”概念，多根的特殊情况得以解决^[6]。

Lambert "W" 函數於基礎物理問題之應用並未完全即使標準情況如 (1) 最近在原子，分子，與光學物理領域可見。^[7]

图象

• 朗伯W函数在复平面上的图像


• 
  

  

  
  

  
  

  z = Re(W₀(x + i y))
  

  
  

  
  


• 
  

  

  
  

  
  

  z = Im(W₀(x + i y))
  

  
  

  
  


• 
  

  

  
  

  
  

  
  


• 
  

  

  
  

  
  

  
  

计算

W函数可以用以下的递推关系算出：

wj+1=wj−wjewj−zewj(wj+1)−(wj+2)(wjewj−z)2wj+2{displaystyle w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}(w_{j}+1)-{frac {(w_{j}+2)(w_{j}e^{w_{j}}-z)}{2w_{j}+2}}}}}

参考来源

1. 
   ^ T.C. Scott and R.B. Mann, General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function, AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 17, no. 1, (April 2006), pp.41-47, [1]; Arxiv [2]
   


2. 
   ^ T.C. Scott, G. Fee and J. Grotendorst, "Asymptotic series of Generalized Lambert W Function", SIGSAM, vol. 47, no. 3, (September 2013), pp. 75-83
   


3. 
   ^ T.C. Scott, G. Fee, J. Grotendorst and W.Z. Zhang, "Numerics of the Generalized Lambert W Function", SIGSAM, vol. 48, no. 2, (June 2014), pp. 42-56
   


4. 
   ^ P.S. Farrugia, R.B. Mann, and T.C. Scott, N-body Gravity and the Schrödinger Equation, Class. Quantum Grav. vol. 24, (2007), pp. 4647-4659, [3]; Arxiv [4]
   


5. 
   ^ T.C. Scott, M. Aubert-Frécon and J. Grotendorst, New Approach for the Electronic Energies of the Hydrogen Molecular Ion, Chem. Phys. vol. 324, (2006), pp. 323-338, [5]; Arxiv [6]
   


6. 
   ^ Aude Maignan, T.C. Scott, "Fleshing out the Generalized Lambert W Function", SIGSAM, vol. 50, no. 2, (June 2016), pp. 45-60
   


7. 
   ^ T.C. Scott, A. Lüchow, D. Bressanini and J.D. Morgan III, The Nodal Surfaces of Helium Atom Eigenfunctions, Phys. Rev. A 75, (2007), p. 060101, [7]
   

外部链接

• MathWorld

This page is only for reference, If you need detailed information, please check here