Mixing
三角函数
三角函数： 正弦、 餘弦、 正切、 餘割（鏈線）、 正割（鏈線）、 餘切（鏈線）
| 三角学 |
|---|
历史 三角函数 广义三角函数 反三角函数 |
参考 |
恒等式 精确值 三角表 |
定理 |
正弦定理 餘弦定理 正切定理 餘切定理 正割定理 餘割定理 勾股定理 |
微积分 |
三角换元法 三角函数的积分 三角函数的微分 反三角函数的积分 |
三角函数（英语：Trigonometric functions）是数学中常见的一类关于角度的函数。三角函数将直角三角形的内角和它的两个边的比值相关联，也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具[1]。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。
常见的三角函数包括正弦函数（sin{displaystyle sin }
三角函数一般用于计算三角形中未知长度的边和未知的角度，在导航、工程学以及物理学方面都有广泛的用途。另外，以三角函数为模版，可以定义一类相似的函数，叫做双曲函数[2]。常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
目录
1 历史
2 几何定义
2.1 直角三角形中的定义
2.2 直角坐标系中的定义
2.3 单位圆定义
3 基本性质
3.1 三角恒等式
3.2 微积分
4 分析学定义
4.1 級數定義
4.1.1 与指数函数和复数的联系
4.2 较少見的三角函數
4.3 微分方程定义
4.3.1 弧度的重要性
4.4 利用函数方程定义三角函数
5 计算
5.1 三角函数的特殊值
6 反三角函数
7 相关定理
7.1 正弦定理
7.2 余弦定理
7.3 正切定理
7.4 餘切定理
7.5 正割定理
7.6 周期函数
8 参见
9 注释
10 参考文献
11 外部链接
历史
早期对于三角函数的研究可以追溯到古代。例如古埃及数学家在鑑別尼羅河泛濫後的土地邊界、保持金字塔每邊斜度相同，都使用了三角術，只是他們可能還沒有對這種方式定名而已。古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。他按照古巴比伦人的做法，将圆周分为360等份（即圆周的弧度为360度，与现代的弧度制不同）。对于给定的弧度，他给出了对应的弦的长度数值，这个记法和现代的正弦函数是等价的。喜帕恰斯实际上给出了最早的三角函数数值表。然而古希腊的三角学基本是球面三角学。这与古希腊人研究的主体是天文学有关。梅涅劳斯在他的著作《球面学》中使用了正弦来描述球面的梅涅劳斯定理。古希腊三角学与其天文学的应用在埃及的托勒密时代达到了高峰，托勒密在《数学汇编》（Syntaxis Mathematica）中计算了36度角和72度角的正弦值，还给出了计算和角公式和半角公式的方法。托勒密还给出了所有0到180度的所有整数和半整数弧度对应的正弦值[3]:133-140[4]:151-152。
希腊文化传播到古印度后，印度人对三角术进行了进一步的研究。公元5世纪末的数学家阿耶波多提出用弧对应的弦长的一半来对应半弧的正弦，这个做法被後来的古印度数学家使用，和现代的正弦定义一致了[4]:189。阿耶波多的计算中也使用了余弦和正割。他在计算弦长时使用了不同的单位，重新计算了0到90度中间隔三又四分之三度（3.75°）的三角函数值表[4]:193。然而古印度的数学与当时的中国一样，停留在计算方面，缺乏系统的定义和演绎的证明。阿拉伯人也采用了古印度人的正弦定义，但他们的三角学是直接继承于古希腊。阿拉伯天文学家引入了正切和余切、正割和余割的概念，并计算了间隔10分（10′）的正弦和正切数值表[3]:214-215。到了公元14世纪，阿拉伯人将三角计算重新以算术方式代数化（古希腊人采用的是建立在几何上的推导方式）的努力为後来三角学从天文学中独立出来，成为了有更广泛应用的学科奠定了基础。[3]:225
进入15世纪后，阿拉伯数学文化开始传入欧洲。随着欧洲商业的兴盛，航行、历法测定和地理测绘中出现了对三角学的需求。在翻译阿拉伯数学著作的同时，欧洲数学家开始制作更详细精确的三角函数值表。哥白尼的学生乔治·约阿希姆·瑞提克斯制作了间隔10秒（10″）的正弦表，有9位精确值。瑞提克斯还改变了正弦的定义，原来称弧对应的弦长是正弦，瑞提克斯则将角度对应的弦长称为正弦。16世纪后，数学家开始将古希腊有关球面三角的结果和定理转化为平面三角定理。弗朗索瓦·韦达给出了托勒密的不少结果对应的平面三角形式。他还尝试计算了多倍角正弦的表达方式。[3]:275-278
18世纪开始，随着解析几何等分析学工具的引进，数学家们开始对三角函数进行分析学上的研究。牛顿在1669年的《分析学》一书中给出了正弦和余弦函数的无穷级数表示。Collins将牛顿的结果告诉了詹姆斯·格列高里，後者进一步给出了正切等三角函数的无穷级数。莱布尼兹在1673年左右也独立得到了这一结果[5]:162-163。欧拉的《无穷小量分析引论》（Introductio in Analysin Infinitorum，1748年）对建立三角函数的分析处理做了最主要的贡献，他定义三角函数为无穷级数，并表述了欧拉公式，还有使用接近现代的简写sin.、cos.、tang.、cot.、sec.和cosec.。
几何定义
直角三角形中的定义
a, b, h分別為角A的对边、邻边和斜边
在直角三角形中仅有锐角（大小在0到90度之间的角）三角函数的定义[6]。给定一个锐角θ{displaystyle theta }
θ{displaystyle theta } 的正弦是对边与斜边的比值：sinθ=ah{displaystyle sin {theta }={frac {a}{h}}} |
θ{displaystyle theta } 的餘弦是邻边与斜边的比值：cosθ=bh{displaystyle cos {theta }={frac {b}{h}}} |
θ{displaystyle theta } 的正切是对边与邻边的比值：tanθ=ab{displaystyle tan {theta }={frac {a}{b}}} |
θ{displaystyle theta } 的余切是邻边与对边的比值：cotθ=ba{displaystyle cot {theta }={frac {b}{a}}} |
θ{displaystyle theta } 的正割是斜边与邻边的比值：secθ=hb{displaystyle sec {theta }={frac {h}{b}}} |
θ{displaystyle theta } 的餘割是斜边与对边的比值：cscθ=ha{displaystyle csc {theta }={frac {h}{a}}} |
直角坐标系中的定义
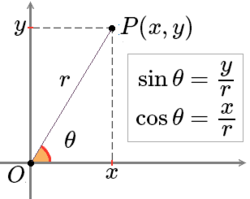
设P(x,y){displaystyle P(x,y)}
| 正弦 | 餘弦 | 正切 | 餘切 | 正割 | 餘割 |
|---|---|---|---|---|---|
sinθ=yr{displaystyle sin theta ={frac {y}{r}}}  | cosθ=xr{displaystyle cos theta ={frac {x}{r}}}  | tanθ=yx{displaystyle tan theta ={frac {y}{x}}}  | cotθ=xy{displaystyle cot theta ={frac {x}{y}}}  | secθ=rx{displaystyle sec theta ={frac {r}{x}}}  | cscθ=ry{displaystyle csc theta ={frac {r}{y}}}  |
这样可以对0到360度的角度定义三角函数。要注意的是以上的定义都只在定义式有意义的时候成立。比如说当x=0{displaystyle x=0}
的时候，yx{displaystyle {frac {y}{x}}}
单位圆定义
三角函数也可以依据直角坐标系xOy{displaystyle xOy}
| 正弦 | 餘弦 | 正切 | 餘切 | 正割 | 餘割 |
|---|---|---|---|---|---|
sinθ=y{displaystyle sin theta =y}  | cosθ=x{displaystyle cos theta =x}  | tanθ=yx{displaystyle tan theta ={frac {y}{x}}} | cotθ=xy{displaystyle cot theta ={frac {x}{y}}} | secθ=1x{displaystyle sec theta ={frac {1}{x}}}  | cscθ=1y{displaystyle csc theta ={frac {1}{y}}}  |
用单位圆定义三角函数
这个定义和坐标系的定义类似，但角度θ可以是任何的数值。对于大于360°或小于-360°的角度，可以认为是逆时针（顺时针）旋转了不止一圈。而多转或少转了整数圈不会影响三角函数的取值[8]。如果按弧度制的方式记录角度，将弧长作为三角函数的输入值（360°等于2π{displaystyle 2pi }
- sinθ=sin(θ+2πk),∀θ∈R,k∈Z{displaystyle sin theta =sin left(theta +2pi kright),quad forall theta in mathbb {R} ,;;kin mathbb {Z} }
- cosθ=cos(θ+2πk),∀θ∈R,k∈Z{displaystyle cos theta =cos left(theta +2pi kright),quad forall theta in mathbb {R} ,;;kin mathbb {Z} }
周期函数的最小正周期叫做这个函数的基本周期。正弦、余弦、正割或余割的基本周期是2π{displaystyle 2pi }
基本性质
在直角坐标系平面上f(x) = sin(x)和f(x) = cos(x)函数的图像。
从几何定义中可以推导出很多三角函数的性质。比如说，正弦函数、正切函数、余切函数和余割函数是奇函数，余弦函数和正割函数是偶函数[9]。正弦和余弦函数的图像形状一样（见右图），可以看作是沿坐标横轴平移得到的两个函数。正弦和余弦函数关于x=π4{displaystyle x={frac {pi }{4}}}
三角恒等式
不同的三角函数之间存在很多对任意的角度取值都成立的等式，被称为三角恒等式。其中最著名的是毕达哥拉斯恒等式，它说明对于任何角，正弦的平方加上余弦的平方总是1[1]。这可从斜边为1的直角三角形应用勾股定理得出。用符号形式表示，毕达哥拉斯恒等式为：
- sin2x+cos2x=1.{displaystyle sin ^{2}!x+cos ^{2}!x=1.}
因此可推導出:
- tan2x+1=sec2x.{displaystyle tan ^{2}!x+1=sec ^{2}!x.}
- 1+cot2x=csc2x.{displaystyle 1+cot ^{2}!x=csc ^{2}!x.}
另一个关键的联系是和差公式，它根据两个角度自身的正弦和余弦而给出它们的和与差的正弦和余弦[1]。它们可以用几何的方法使用托勒密的论证方法推导出来；还可以用代数方法使用欧拉公式得出。
|
|
当两个角相同的时候，和角公式简化为更简单的等式，称为二倍角公式（或倍角公式）。
这些等式还可以用来推导积化和差恒等式[10]，以前曾用它把两个数的积变换成两个数的和而像对数那样使运算更加快速。（利用制好的三角函数表）
微积分
三角函数的积分和导数可参见导数表、积分表和三角函数积分表。下面是六個基本三角函數的導數和積分的列表。
| 函数 | sinx{displaystyle , sin x}  | cosx{displaystyle , cos x}  | tanx{displaystyle , tan x}  | cotx{displaystyle , cot x}  | secx{displaystyle , sec x}  | cscx{displaystyle , csc x}  |
|---|---|---|---|---|---|---|
导函数 | cosx{displaystyle , cos x} | −sinx{displaystyle , -sin x}  | sec2x{displaystyle , sec ^{2}x}  | −csc2x{displaystyle , -csc ^{2}x}  | secxtanx{displaystyle , sec {x}tan {x}}  | −cscxcotx{displaystyle , -csc {x}cot {x}}  |
原函数* | −cosx{displaystyle , -cos x}  | sinx{displaystyle , sin x} | −ln|cosx|{displaystyle , -ln left|cos xright|}  | ln|sinx|{displaystyle ln left|sin xright|}  | ln|secx+tanx|{displaystyle ln left|sec x+tan xright|}  | ln|cscx−cotx|{displaystyle ln left|csc x-cot xright|}  |
* 不计常数项 | ||||||
分析学定义
級數定義
正弦函数（蓝色）十分接近于它的7次泰勒级数（粉红色）。
几何学中，三角函数的定义是建立在几何直观上的，只用几何和极限的性质，就可直接获知正弦和餘弦的導數。分析学中，三角函數是解析函數，数学家用泰勒級數给出了不依赖几何直观的代数定义[11]：
- sinx=∑n=0∞(−1)nx2n+1(2n+1)!=x−x33!+x55!−x77!+⋯{displaystyle sin x=sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots }
- cosx=∑n=0∞(−1)nx2n(2n)!=1−x22!+x44!−x66!+⋯{displaystyle cos x=sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n}}{(2n)!}}=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-{frac {x^{6}}{6!}}+cdots }
可以证明以上的无穷级数对任意实数x{displaystyle x}
三角函数的级数定义经常被用做三角函数的严格处理和应用的起点（比如，在傅立叶级数中），因为无穷级数的理论可从实数系的基础上发展而来，不需要任何几何方面的考虑。这样，这些函数的可微性和连续性便可以单独从级数定义来确立。
其他三角函数的级数定义：[12]
- tanx=∑n=1∞(−1)n−122n(22n−1)B2nx2n−1(2n)!=x+x33+2x515+17x7315+⋯(|x|<π2){displaystyle tan x=sum _{n=1}^{infty }{frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x+{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}+{frac {17x^{7}}{315}}+cdots left(|x|<{frac {pi }{2}}right)}
- cscx=∑n=0∞(−1)n+12(22n−1−1)B2nx2n−1(2n)!=1x+x6+7x3360+31x515120+⋯(0<|x|<π){displaystyle csc x=sum _{n=0}^{infty }{frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}={frac {1}{x}}+{frac {x}{6}}+{frac {7x^{3}}{360}}+{frac {31x^{5}}{15120}}+cdots (0<|x|<pi )}
- secx=∑n=0∞(−1)nEnx2n(2n)!=1+x22+5x424+61x6720+⋯(|x|<π2){displaystyle sec x=sum _{n=0}^{infty }{frac {(-1)^{n}E_{n}x^{2n}}{(2n)!}}=1+{frac {x^{2}}{2}}+{frac {5x^{4}}{24}}+{frac {61x^{6}}{720}}+cdots left(|x|<{frac {pi }{2}}right)}
- cotx=∑n=0∞(−1)n22nB2nx2n−1(2n)!=1x−x3−x345−2x5945−⋯(0<|x|<π){displaystyle cot x=sum _{n=0}^{infty }{frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}={frac {1}{x}}-{frac {x}{3}}-{frac {x^{3}}{45}}-{frac {2x^{5}}{945}}-cdots (0<|x|<pi )}
其中Bn{displaystyle B_{n},}
这些定义也可以看作是每个三角函数作为实函数的泰勒级数。从复分析的一个定理得出，这个实函数到复数有一个唯一的解析扩展。它们有同样的泰勒级数，所以复数上的三角函数是使用上述级数来定义的。
与指数函数和复数的联系
可以从上述的级数定义证明正弦和余弦函数分别是复指数函数在它的自变量为纯虚数时候的虚数和实数部分：
eiθ=cosθ+isinθ.{displaystyle e^{{mathrm {i} }theta }=cos theta +{mathrm {i} }sin theta ,.}（
i是虚数单位）
这个关系式首先被欧拉注意到，因此叫做欧拉公式[13] 。从中可推出，对实数x，
- cosx=Re(eix),sinx=Im(eix){displaystyle cos x,=,operatorname {Re} ;left(e^{{mathrm {i} }x}right);;,qquad quad sin x,=,operatorname {Im} ;left(e^{{mathrm {i} }x}right)}
进一步还可以定义对复自变量z的三角函数：
- sinz=∑n=0∞(−1)n(2n+1)!z2n+1=eiz−e−iz2i=−isinh(iz){displaystyle sin z,=,sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}z^{2n+1},=,{e^{{mathrm {i} }z}-e^{-{mathrm {i} }z} over 2{mathrm {i} }}=-{mathrm {i} }sinh left({mathrm {i} }zright)}
- cosz=∑n=0∞(−1)n(2n)!z2n=eiz+e−iz2=cosh(iz){displaystyle cos z,=,sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}z^{2n},=,{e^{{mathrm {i} }z}+e^{-{mathrm {i} }z} over 2}=cosh left({mathrm {i} }zright)}
- sin(a+bi)=sinacoshb+(cosasinhb)i{displaystyle sin(a+bmathrm {i} )=sin acosh b+(cos asinh b)mathrm {i} }
- cos(a+bi)=cosacoshb−(sinasinhb)i{displaystyle cos(a+bmathrm {i} )=cos acosh b-(sin asinh b)mathrm {i} }
- tan(a+bi)=tana+(tanhb)i1−(tanatanhb)i{displaystyle tan(a+bmathrm {i} )={frac {tan a+(tanh b)mathrm {i} }{1-(tan atanh b)mathrm {i} }}}
 |  |  |  |  |  |
sin(z){displaystyle sin(z)}  | cos(z){displaystyle cos(z)}  | tan(z){displaystyle tan(z)}  | cot(z){displaystyle cot(z)}  | sec(z){displaystyle sec(z)}  | csc(z){displaystyle csc(z)}  |
较少見的三角函數
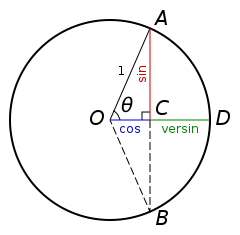
除了上述六個基本函數，历史上還有下列幾个较少見的三角函数：
正矢 | versinθ=1−cosθ{displaystyle mathrm {versin} ;theta =1-cos theta }  | 半正矢 | haversinθ=1−cosθ2{displaystyle mathrm {haversin} ;theta ={frac {1-cos theta }{2}}}  |
vercosinθ=1+cosθ{displaystyle mathrm {vercosin} ;theta =1+cos theta }  | havercosinθ=1+cosθ2{displaystyle mathrm {havercosin} ;theta ={frac {1+cos theta }{2}}}  | ||
餘矢 | coversinθ=1−sinθ{displaystyle mathrm {coversin} ;theta =1-sin theta }  | 半餘矢 | hacoversinθ=1−sinθ2{displaystyle mathrm {hacoversin} ;theta ={frac {1-sin theta }{2}}}  |
covercosinθ=1+sinθ{displaystyle mathrm {covercosin} ;theta =1+sin theta }  | hacovercosinθ=1+sinθ2{displaystyle mathrm {hacovercosin} ;theta ={frac {1+sin theta }{2}}}  | ||
外正割 | exsecθ=secθ−1{displaystyle mathrm {exsec} ;theta =sec theta -1}  | 外餘割 | excscθ=cscθ−1{displaystyle mathrm {excsc} ;theta =csc theta -1}  |
微分方程定义
正弦和余弦函数都满足微分方程
- y″+y=0{displaystyle y''+y=0,}
就是说，它们加上自己的二阶导数都等于0函数。在由所有这个方程的解的二维向量空间V{displaystyle V}
正切函数是非线性微分方程
- y′=1+y2{displaystyle y'=1+y^{2},}
满足初始条件y(0)=0{displaystyle y(0)=0}
弧度的重要性
弧度通过测量沿着单位圆的路径的长度而指定一个角，并构成正弦和余弦函数的特定辐角。特别是，只有映射弧度到比率的那些正弦和余弦函数才满足描述它们的经典微分方程。如果正弦和余弦函数的弧度辐角是正比于频率的
- f(x)=sin(kx);k≠0,k≠1{displaystyle f(x)=sin(kx);kneq 0,kneq 1,}
则导数将正比于“振幅”。
f′(x)=kcos(kx){displaystyle f'(x)=kcos(kx),}.
这里的k是表示在单位之间映射的常数。如果x是度，则
- k=π180∘.{displaystyle k={frac {pi }{180^{circ }}}.}
如果x是圈（轉，2π{displaystyle 2pi }
- k=2π{displaystyle k=2pi }
这意味着使用度（或圈）的正弦的二阶导数不满足微分方程
y″=−y{displaystyle y''=-y,}
但满足
y″=−k2y{displaystyle y''=-k^{2}y,};
对余弦也是类似的。
这意味着这些正弦和余弦是不同的函数，因此只有它的辐角是弧度的条件下，正弦的四阶导数才再次是正弦。
利用函数方程定义三角函数
在数学分析中，可以利用基于和差公式这样的性质的函数方程来定义三角函数。例如，取用给定此种公式和毕达哥拉斯恒等式，可以证明只有两个实函数满足这些条件。即存在唯一的一对实函数sin{displaystyle sin }
- sin2x+cos2x=1,{displaystyle sin ^{2}!x+cos ^{2}!x=1,,}
- sin(x+y)=sinxcosy+cosxsiny,{displaystyle sin(x+y)=sin !xcos !y+cos !xsin !y,,}
- cos(x+y)=cosxcosy−sinxsiny,{displaystyle cos(x+y)=cos !xcos !y-sin !xsin !y,,}
并满足附加条件
0<xcosx<sinx<x for0<x<1{displaystyle 0<x!cos !x<sin !x<x mathrm {for} qquad 0<x<1}.
从其他函数方程开始的推导也是可能的，这种推导可以扩展到复数。作为例子，这个推导可以用来定义伽罗瓦域中的三角学。
计算
三角函数的计算是个复杂的主题，由于计算机和提供对任何角度的内置三角函数的科学计算器的广泛使用，现在大多数人都不需要了。本节中将描述它在三个重要背景下的计算详情：历史上三角函数表的使用，计算机使用的现代技术，以及容易找到简单精确值的一些“重要”角度。（下面只考虑一个角度小范围，比如0到π2{displaystyle {frac {pi }{2}}}
有计算机之前，人们通常通过对计算到多个有效数字的三角函数表的内插来计算三角函数的值。这种表格在人们刚刚产生三角函数的概念的时候就已经有了，它们通常是通过从已知值（比如sinπ2=1{displaystyle sin {frac {pi }{2}}=1}
现代计算机使用了各种技术。[18]一个常见的方式，特别是在有浮点单元的高端处理器上，是组合多项式或有理式逼近（比如切比雪夫逼近、最佳一致逼近和Padé逼近，和典型用于更高或可变精度的泰勒级数和罗朗级数）和范围简约与表查找—首先在一个较小的表中查找最接近的角度，然后使用多项式来计算修正。[19]在缺乏硬件乘法器的简单设备上，有叫做CORDIC算法的一个更有效算法（和相关技术），因为它只用了移位和加法。出于性能的原因，所有这些方法通常都用硬件来实现。
对于非常高精度的运算，在级数展开收敛变得太慢的时候，可以用算术几何平均来逼近三角函数，它自身通过复数椭圆积分来逼近三角函数。[20]
三角函数的特殊值
如图所示，大小为 30∘{displaystyle 30^{circ }}
和 45∘{displaystyle 45^{circ }}
的整数倍的θ{displaystyle theta }角和它们的精确正弦和余弦值已被标注在单位圆上。θ{displaystyle theta }角均用弧度制和角度制表示。θ{displaystyle theta }角所对应的单位圆上的点的坐标为（cosθ{displaystyle cos theta }
，sinθ{displaystyle sin theta }
）。对于一些简单的角度，使用毕达哥拉斯定理（也就是勾股定理）可以很容易手工计算三角函数的值。事实上，π/60{displaystyle pi /60}
| 函数名 | 0 (0∘){displaystyle 0 (0^{circ })}  | π12 (15∘){displaystyle {frac {pi }{12}} (15^{circ })}  | π6 (30∘){displaystyle {frac {pi }{6}} (30^{circ })}  | π4 (45∘){displaystyle {frac {pi }{4}} (45^{circ })}  | π3 (60∘){displaystyle {frac {pi }{3}} (60^{circ })}  | 5π12 (75∘){displaystyle {frac {5pi }{12}} (75^{circ })}  | π2 (90∘){displaystyle {frac {pi }{2}} (90^{circ })}  |
|---|---|---|---|---|---|---|---|
sin{displaystyle sin } | 0{displaystyle 0}  | 6−24{displaystyle {frac {{sqrt {6}}-{sqrt {2}}}{4}}}  | 12{displaystyle {frac {1}{2}}}  | 22{displaystyle {frac {sqrt {2}}{2}}}  | 32{displaystyle {frac {sqrt {3}}{2}}}  | 6+24{displaystyle {frac {{sqrt {6}}+{sqrt {2}}}{4}}}  | 1{displaystyle 1}  |
cos{displaystyle cos } | 1{displaystyle 1} | 6+24{displaystyle {frac {{sqrt {6}}+{sqrt {2}}}{4}}} | 32{displaystyle {frac {sqrt {3}}{2}}} | 22{displaystyle {frac {sqrt {2}}{2}}} | 12{displaystyle {frac {1}{2}}} | 6−24{displaystyle {frac {{sqrt {6}}-{sqrt {2}}}{4}}} | 0{displaystyle 0} |
tan{displaystyle tan } | 0{displaystyle 0} | 2−3{displaystyle 2-{sqrt {3}}}  | 33{displaystyle {frac {sqrt {3}}{3}}}  | 1{displaystyle 1} | 3{displaystyle {sqrt {3}}}  | 2+3{displaystyle 2+{sqrt {3}}}  | ±∞{displaystyle pm infty }  |
cot{displaystyle cot } | ±∞{displaystyle pm infty } | 2+3{displaystyle 2+{sqrt {3}}} | 3{displaystyle {sqrt {3}}} | 1{displaystyle 1} | 33{displaystyle {frac {sqrt {3}}{3}}} | 2−3{displaystyle 2-{sqrt {3}}} | 0{displaystyle 0} |
sec{displaystyle sec } | 1{displaystyle 1} | 6−2{displaystyle {sqrt {6}}-{sqrt {2}}}  | 233{displaystyle {frac {2{sqrt {3}}}{3}}}  | 2{displaystyle {sqrt {2}}}  | 2{displaystyle 2}  | 6+2{displaystyle {sqrt {6}}+{sqrt {2}}}  | ±∞{displaystyle pm infty } |
csc{displaystyle csc } | ±∞{displaystyle pm infty } | 6+2{displaystyle {sqrt {6}}+{sqrt {2}}} | 2{displaystyle 2} | 2{displaystyle {sqrt {2}}} | 233{displaystyle {frac {2{sqrt {3}}}{3}}} | 6−2{displaystyle {sqrt {6}}-{sqrt {2}}} | 1{displaystyle 1} |
注：有时候±∞{displaystyle pm infty }
反三角函数
由於三角函数属于周期函数，而不是单射函数，所以严格来说并没有反函数。因此要定义其反函数必须先限制三角函数的定义域，使得三角函数成为双射函数。基本的反三角函数定义为[9]：
| 反三角函数 | 定义 | 值域 |
|---|---|---|
arcsin(x)=y{displaystyle arcsin(x)=y,}  | sin(y)=x{displaystyle sin(y)=x,}  | −π2≤y≤π2{displaystyle -{frac {pi }{2}}leq yleq {frac {pi }{2}},}  |
arccos(x)=y{displaystyle arccos(x)=y,}  | cos(y)=x{displaystyle cos(y)=x,}  | 0≤y≤π{displaystyle 0leq yleq pi ,}  |
arctan(x)=y{displaystyle arctan(x)=y,}  | tan(y)=x{displaystyle tan(y)=x,}  | −π2<y<π2{displaystyle -{frac {pi }{2}}<y<{frac {pi }{2}},}  |
arccsc(x)=y{displaystyle operatorname {arccsc}(x)=y,}  | csc(y)=x{displaystyle csc(y)=x,}  | −π2≤y≤π2,y≠0{displaystyle -{frac {pi }{2}}leq yleq {frac {pi }{2}},yneq 0,}  |
arcsec(x)=y{displaystyle operatorname {arcsec}(x)=y,}  | sec(y)=x{displaystyle sec(y)=x,}  | 0≤y≤π,y≠π2{displaystyle 0leq yleq pi ,yneq {frac {pi }{2}},}  |
arccot(x)=y{displaystyle operatorname {arccot}(x)=y,}  | cot(y)=x{displaystyle cot(y)=x,}  | 0<y<π{displaystyle 0<y<pi ,}  |
对于反三角函数，符号sin−1{displaystyle sin ^{-1}}
正如正弦和余弦那样，反三角函数也可以根据无穷级数来定义。例如，
- arcsinz=z+(12)z33+(1⋅32⋅4)z55+(1⋅3⋅52⋅4⋅6)z77+⋯{displaystyle arcsin z=z+left({frac {1}{2}}right){frac {z^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {z^{5}}{5}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {z^{7}}{7}}+cdots }
这些函数也可以通过证明它们是其他函数的原函数来定义。例如反正弦函数，可以写为如下积分[22]：
- arcsin(x)=∫0x11−z2dz,|x|<1{displaystyle arcsin left(xright)=int _{0}^{x}{frac {1}{sqrt {1-z^{2}}}},mathrm {d} z,quad |x|<1}
可以在反三角函数条目中找到类似的公式。使用复对数，可以把这些函数推广到复数辐角上：
- arcsin(z)=−iln(iz+1−z2){displaystyle arcsin(z)=-{mathrm {i} }ln left({mathrm {i} }z+{sqrt {1-z^{2}}}right)}
- arccos(z)=−iln(z+z2−1){displaystyle arccos(z)=-{mathrm {i} }ln left(z+{sqrt {z^{2}-1}}right)}
- arctan(z)=i2ln(1−iz1+iz){displaystyle arctan(z)={frac {mathrm {i} }{2}}ln left({frac {1-{mathrm {i} }z}{1+{mathrm {i} }z}}right)}
相关定理
三角函数，正如其名称那样，在三角学中是十分重要的。在三角学研究中，数学家们发现了许多利用三角函数来刻画三角形、圆形或多边形的定理。
正弦定理
利萨茹曲线，一种三角基的函数形成的图像。
正弦定理声称对于边长为a{displaystyle a}
- asinA=bsinB=csinC=2R{displaystyle {frac {a}{sin A}}={frac {b}{sin B}}={frac {c}{sin C}}=2R}
其中R{displaystyle R}
余弦定理
余弦定理（也叫做余弦公式）是托勒密定理的推广[23]：
- c2=a2+b2−2abcosC{displaystyle c^{2}=a^{2}+b^{2}-2abcos C}
也可表示为：
cosC=a2+b2−c22ab{displaystyle cos C={frac {a^{2}+b^{2}-c^{2}}{2ab}}}余弦定理用于在一个三角形的两个边和一个角已知时确定未知的数据。
正切定理
还有一个正切定理[24]:
- a+ba−b=tanA+B2tanA−B2{displaystyle {frac {a+b}{a-b}}={frac {tan {dfrac {A+B}{2}}}{tan {dfrac {A-B}{2}}}}}
餘切定理
cotα2=s−aζ{displaystyle cot {frac {alpha }{2}}={frac {s-a}{zeta }}}
正割定理
a=bsecC+csecB{displaystyle a={frac {b}{sec C}}+{frac {c}{sec B}}}
周期函数
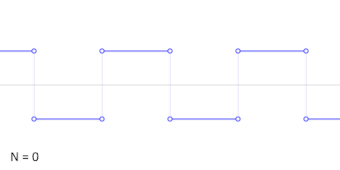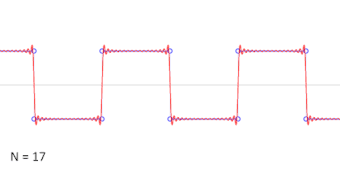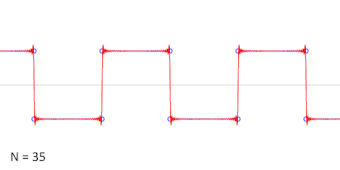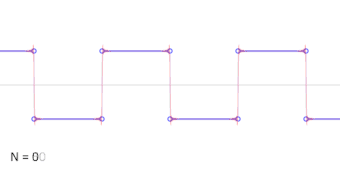
谐波数目递增的方波的加法合成的动画。
三角函数在物理中也是重要的。例如，正弦和余弦函数被用来描述简谐运动，它描述了很多自然现象，比如附着在弹簧上的物体的振动，挂在绳子上物体的小角度摆动。正弦和余弦函数是圆周运动的一维投影[25]。
三角函数在一般周期函数的研究中也很有用。这些函数有作为图像的特征波模式，在描述循环现象比如声波或光波的时候是很有用的。每一个信号都可以记为不同频率的正弦和余弦函数的（通常是无限的）和[26]；这是傅立叶分析的基础想法，这里的三角级数可以用来解微分方程的各种边值问题。例如，方波可以写为傅立叶级数[27]
- xsquare(t)=4π∑k=1∞sin[(2k−1)t](2k−1).{displaystyle x_{mathrm {square} }(t)={frac {4}{pi }}sum _{k=1}^{infty }{sin {left[(2k-1)tright]} over (2k-1)}.}
![x_{{{mathrm {square}}}}(t)={frac {4}{pi }}sum _{{k=1}}^{infty }{sin {left[(2k-1)tright]} over (2k-1)}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a7a67d5fb9c63ea948da8db3bcf03c50433d986)
在右边的动画中，可以看到只用少数的项就已经形成了非常准确的估计。
参见
- 三角函數精確值
- 三角恒等式
- 三角学
- 生成三角函数表
- 双曲函数
- 勾股定理
- 方向余弦
- 欧拉公式
- 诱导公式
注释
^ 1.01.11.21.31.4 萧树铁, 扈志明. 微积分. 北京: 清华大学出版社有限公司. 2006: p.8–9. ISBN 7302122148. 引文格式1维护：冗余文本 (link)}
^ 清华大学数学科学系《微积分》编写组. 微积分（I）. 清华大学出版社. 2003. ISBN 9787302067856.
^ 3.03.13.23.3 莫里斯·克莱因 著，张理京，张锦炎，江泽涵 译. 《古今数学思想》第一册. 上海科学技术出版社. 2002. ISBN 9787532361724.
^ 4.04.14.2 Uta C.Merzbach, Carl B. Boyer. A History of Mathematics. John Wiley & Sons, Inc.第3版. 2011. ISBN 978-0-470-52548-7 （英语）.
^ 莫里斯·克莱因 著，朱学贤，申又枨，叶其孝 译. 《古今数学思想》第二册. 上海科学技术出版社. 2002. ISBN 9787532361731.
^ 銳角三角函數 (PDF). [2013-12-21].
^ 三角函數的定義. Webcai.math.fcu.edu.tw. [2013-12-21].
^ 廣義角三角函數 (PDF). [2013-12-21].
^ 9.09.1 谭杰锋, 郑爱武. 高等数学. 清华大学出版社. 2006.
^ 初三年级. 积化和差公式. Zhongxue.hujiang.com. [2013-12-21].
^ Ahlfors, pages 43–44.
^ Abramowitz; Weisstein.
^ Euler (1707-1783) —數學的莎士比亞 (PDF). [2013-12-21]. （原始内容 (PDF)存档于2007-02-08）.
^ 以微積分方法探討三角函數的性質 (PDF). [2013-12-21].
^ Needham, p. ix.
^ Kannappan, Palaniappan. Functional Equations and Inequalities with Applications. Springer. 2009. ISBN 978-0387894911.
^ 和差角公式. Highscope.ch.ntu.edu.tw. 2011-10-19 [2013-12-21].
^ Kantabutra.
^ However, doing that while maintaining precision is nontrivial, and methods like Gal's accurate tables, Cody and Waite reduction, and Payne and Hanek reduction algorithms can be used.
^ R. P. Brent, "Fast Multiple-Precision Evaluation of Elementary Functions", J. ACM '''23''', 242 (1976). Doi.acm.org. [2013-12-21]. doi:10.1145/321941.321944.
^ 三角函數特殊角的值. Web.ntnu.edu.tw. [2013-12-21].
^ 雙曲函數及反三角函數. Stat.nuk.edu.tw. [2013-12-21].
^ 23.023.1 正弦定理與餘弦定理 (PDF). [2013-12-21].
^ Eli Maor, Trigonometric Delights, Princeton University Press, 2002.
^ 圓與三角學. Episte.math.ntu.edu.tw. 2004-06-19 [2013-12-21].
^ 靳希,杨尔滨,赵玲. 信号处理原理与应用. 清华大学出版社. 2004. ISBN 9787302083573.|chapter=被忽略 (帮助)
^ 邓翔宇. 信号与系统. 清华大学出版社. 2006. ISBN 9787810827058.|chapter=被忽略 (帮助)
参考文献
- Abramowitz, Milton、Irene A. Stegun，Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables，Dover，New York（1964年），ISBN 978-0-486-61272-0。
- Boyer, Carl B.，A History of Mathematics，John Wiley & Sons, Inc.，第二版（1991年），ISBN 978-0-471-54397-8。
- Joseph, George G.，The Crest of the Peacock: Non-European Roots of Mathematics，第二版，Penguin Books，London，（2000年），ISBN 978-0-691-00659-8。
- Kantabutra, Vitit，On hardware for computing exponential and trigonometric functions，IEEE Trans. Computers 45 (3), 328-339（1996年）。
- Maor, Eli，Trigonometric Delights，Princeton Univ. Press.（1998年），重印版（2005年2月25日）：ISBN 978-0-691-09541-7。
- Needham, Tristan，Preface，Visual Complex Analysis，Oxford University Press，（1999年），ISBN 978-0-19-853446-4。
- O'Connor, J.J.、E.F. Robertson，Trigonometric functions，MacTutor History of Mathematics Archive，（1996年）。
- O'Connor, J.J.、E.F. Robertson，Madhava of Sangamagramma，MacTutor History of Mathematics Archive，（2000年）。
- Pearce, Ian G.，Madhava of Sangamagramma，MacTutor History of Mathematics Archive，（2002年）。
- Weisstein, Eric W.，Tangent，MathWorld，2006年1月21日访问。
- Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
外部链接
- Engineers Edge的三角函數列表
nanoSouffle線上繪圖─可繪畫各種函數。可在各瀏覽器使用，JavaScript只用於實時更新，並非必須
正弦和餘弦函數─以REXX來表示
以角度和弧度表示的角所對應的函數值[永久失效連結]
- 單位圓教學Flash動畫
- 常用三角函數表（文字版）
| |||||||||||||||||||||||||||||
|
Comments
Post a Comment