引力場
| 本條目需要擴充。 (2015年4月8日) |
引力場(簡體中文中重力場一詞特指地球表面的引力場。)是描述一物体在空間中受到万有引力(重力)作用的場[1],在经典物理学中是一个物理量[2]。
目录
1 科普概念
2 计算方法
3 参考资料
4 參閲
科普概念
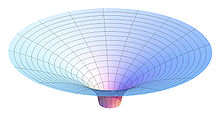
引力场的不完全示意图
所有有質量的物體皆會互相吸引。我們想像空間是一張水平面,在上面放上一質量A,A會使此平面向下凹陷,質量越大則凹陷越深;當你放下第二質量B時,B便順著A的凹陷滾向A,使兩物體在空間上靠近。這樣的凹陷便是「重力場」,不同質量會創造的凹陷程度不同,也就是創造的重力場強度不同。
重力場與重力獨立運作,可以想像上述的物質B換成更重的物質C,則AC接近的趨勢將大於AB接近的趨勢,那樣的「趨勢」就是「重力」。
綜觀而言,物體A產生的重力場,只與A本身的質量有關係。至於重力大小是多少,則決定於BCDE...等等其他物質的質量大小。我們便用一個方便的方式記錄這樣的重力場:把A之外的另一個物質質量當成1(即單位質量),這樣便可以直接把算出來的重力場乘以其他物質的質量,簡單而快速地算出兩者之間的重力。
计算方法
任何有質量荷的物體都會產生、響應引力場。我们用引力場強度描述引力场与物体间相互作用的性质。
引力場強度定義為:E=Fm{displaystyle mathbf {E} ={frac {mathbf {F} }{m}}}
其中,F是質點m在場中受到的引力。由萬有引力定律:F=Gm1m2r3r{displaystyle mathbf {F} =G{frac {m_{1}m_{2}}{r^{3}}}mathbf {r} }
不妨將其寫作:E=Gmr3r{displaystyle mathbf {E} =G{frac {m}{r^{3}}}mathbf {r} }
這裡m是產生引力場的物體質量(此處應看作質點及質點質量)、r是兩物體之間的位矢,r为其模量,G是萬有引力常數。需要注意的是,这里的r为矢量,故不同于一般认为的标量式,分母处的模r应为三次方,而分子处为矢量。在标量式中,此处可以化简,故分母处为二次方。
引力場強度的量綱为L/T2{displaystyle L/T^{2}}
参考资料
^ Richard Feynman. The Feynman Lectures on Physics Vol I. Addison Wesley Longman. 1970. ISBN 978-0-201-02115-8.
^ Richard Feynman. The Feynman Lectures on Physics Vol II. Addison Wesley Longman. 1970. ISBN 978-0-201-02115-8.A “field” is any physical quantity which takes on different values at different points in space.
參閲
- 經典力學
- 牛頓運動定律
- 牛頓萬有引力定律
- 拉普拉斯-龍格-冷次向量
- 廣義相對論
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||




Comments
Post a Comment