Residue theorem



























Mathematical analysis → Complex analysis
Complex analysis
Gamma abs 3D.png

Complex numbers


  • Real number

  • Imaginary number

  • Complex plane

  • Complex conjugate

  • Unit complex number

Complex functions


  • Complex-valued function

  • Analytic function

  • Holomorphic function

  • Cauchy–Riemann equations

  • Formal power series

Basic Theory


  • Zeros and poles

  • Cauchy's integral theorem

  • Local primitive

  • Cauchy's integral formula

  • Winding number

  • Laurent series

  • Isolated singularity

  • Residue theorem

  • Conformal map

  • Schwarz lemma

  • Harmonic function

  • Laplace's equation

Geometric function theory

People


  • Augustin-Louis Cauchy

  • Leonhard Euler

  • Carl Friedrich Gauss

  • Jacques Hadamard

  • Kiyoshi Oka

  • Bernhard Riemann

  • Karl Weierstrass


  • Nuvola apps kmplot.svg Analysis portal


  • v

  • t

  • e


In complex analysis, a discipline within mathematics, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. From a geometrical perspective, it is a special case of the generalized Stokes' theorem.




Contents






  • 1 Statement


  • 2 Examples


    • 2.1 An integral along the real axis


    • 2.2 An infinite sum




  • 3 See also


  • 4 References


  • 5 External links





Statement


The statement is as follows:




Illustration of the setting.


Let U be a simply connected open subset of the complex plane containing a finite list of points a1, ..., an, and f a function defined and holomorphic on U {a1, ..., an}. Let γ be a closed rectifiable curve in U which does not meet any of the ak, and denote the winding number of γ around ak by I(γ, ak). The line integral of f around γ is equal to 2πi times the sum of residues of f at the points, each counted as many times as γ winds around the point:


∮γ⁡f(z)dz=2πi∑k=1nI⁡(γ,ak)Res⁡(f,ak).{displaystyle oint _{gamma }f(z),dz=2pi isum _{k=1}^{n}operatorname {I} (gamma ,a_{k})operatorname {Res} (f,a_{k}).}{displaystyle oint _{gamma }f(z),dz=2pi isum _{k=1}^{n}operatorname {I} (gamma ,a_{k})operatorname {Res} (f,a_{k}).}

If γ is a positively oriented simple closed curve, I(γ, ak) = 1 if ak is in the interior of γ, and 0 if not, so


∮γ⁡f(z)dz=2πi∑Res⁡(f,ak){displaystyle oint _{gamma }f(z),dz=2pi isum operatorname {Res} (f,a_{k})}{displaystyle oint _{gamma }f(z),dz=2pi isum operatorname {Res} (f,a_{k})}

with the sum over those ak inside γ.


The relationship of the residue theorem to Stokes' theorem is given by the Jordan curve theorem. The general plane curve γ must first be reduced to a set of simple closed curves {γi} whose total is equivalent to γ for integration purposes; this reduces the problem to finding the integral of f dz along a Jordan curve γi with interior V. The requirement that f be holomorphic on U0 = U {ak} is equivalent to the statement that the exterior derivative d(f dz) = 0 on U0. Thus if two planar regions V and W of U enclose the same subset {aj} of {ak}, the regions V W and W V lie entirely in U0, and hence


∫V∖Wd(fdz)−∫W∖Vd(fdz){displaystyle int _{Vsmallsetminus W}d(f,dz)-int _{Wsmallsetminus V}d(f,dz)}{displaystyle int _{Vsmallsetminus W}d(f,dz)-int _{Wsmallsetminus V}d(f,dz)}

is well-defined and equal to zero. Consequently, the contour integral of f dz along γj = ∂V is equal to the sum of a set of integrals along paths λj, each enclosing an arbitrarily small region around a single aj — the residues of f (up to the conventional factor 2πi) at {aj}. Summing over {γj}, we recover the final expression of the contour integral in terms of the winding numbers {I(γ, ak)}.


In order to evaluate real integrals, the residue theorem is used in the following manner: the integrand is extended to the complex plane and its residues are computed (which is usually easy), and a part of the real axis is extended to a closed curve by attaching a half-circle in the upper or lower half-plane, forming a semicircle. The integral over this curve can then be computed using the residue theorem. Often, the half-circle part of the integral will tend towards zero as the radius of the half-circle grows, leaving only the real-axis part of the integral, the one we were originally interested in.



Examples



An integral along the real axis


The integral


∫−∞∞eitxx2+1dx{displaystyle int _{-infty }^{infty }{frac {e^{itx}}{x^{2}+1}},dx}{displaystyle int _{-infty }^{infty }{frac {e^{itx}}{x^{2}+1}},dx}



The contour C.


arises in probability theory when calculating the characteristic function of the Cauchy distribution. It resists the techniques of elementary calculus but can be evaluated by expressing it as a limit of contour integrals.


Suppose t > 0 and define the contour C that goes along the real line from −a to a and then counterclockwise along a semicircle centered at 0 from a to −a. Take a to be greater than 1, so that the imaginary unit i is enclosed within the curve. Now consider the contour integral


∫Cf(z)dz=∫Ceitzz2+1dz.{displaystyle int _{C}{f(z)},dz=int _{C}{frac {e^{itz}}{z^{2}+1}},dz.}{displaystyle int _{C}{f(z)},dz=int _{C}{frac {e^{itz}}{z^{2}+1}},dz.}

Since eitz is an entire function (having no singularities at any point in the complex plane), this function has singularities only where the denominator z2 + 1 is zero. Since z2 + 1 = (z + i)(z − i), that happens only where z = i or z = −i. Only one of those points is in the region bounded by this contour. Because f(z) is


eitzz2+1=eitz2i(1z−i−1z+i)=eitz2i(z−i)−eitz2i(z+i),{displaystyle {begin{aligned}{frac {e^{itz}}{z^{2}+1}}&={frac {e^{itz}}{2i}}left({frac {1}{z-i}}-{frac {1}{z+i}}right)\&={frac {e^{itz}}{2i(z-i)}}-{frac {e^{itz}}{2i(z+i)}},end{aligned}}}{begin{aligned}{frac {e^{itz}}{z^{2}+1}}&={frac {e^{itz}}{2i}}left({frac {1}{z-i}}-{frac {1}{z+i}}right)\&={frac {e^{itz}}{2i(z-i)}}-{frac {e^{itz}}{2i(z+i)}},end{aligned}}

the residue of f(z) at z = i is


Resz=i⁡f(z)=e−t2i.{displaystyle operatorname {Res} limits _{z=i}f(z)={frac {e^{-t}}{2i}}.}{displaystyle operatorname {Res} limits _{z=i}f(z)={frac {e^{-t}}{2i}}.}

According to the residue theorem, then, we have


∫Cf(z)dz=2πi⋅Resz=i⁡f(z)=2πie−t2i=πe−t.{displaystyle int _{C}f(z),dz=2pi icdot operatorname {Res} limits _{z=i}f(z)=2pi i{frac {e^{-t}}{2i}}=pi e^{-t}.}{displaystyle int _{C}f(z),dz=2pi icdot operatorname {Res} limits _{z=i}f(z)=2pi i{frac {e^{-t}}{2i}}=pi e^{-t}.}

The contour C may be split into a straight part and a curved arc, so that


∫straightf(z)dz+∫arcf(z)dz=πe−t{displaystyle int _{mathrm {straight} }f(z),dz+int _{mathrm {arc} }f(z),dz=pi e^{-t},}int _{mathrm {straight} }f(z),dz+int _{mathrm {arc} }f(z),dz=pi e^{-t},

and thus


∫−aaf(z)dz=πe−t−∫arcf(z)dz.{displaystyle int _{-a}^{a}f(z),dz=pi e^{-t}-int _{mathrm {arc} }f(z),dz.}int _{-a}^{a}f(z),dz=pi e^{-t}-int _{mathrm {arc} }f(z),dz.

Using some estimations, we have


|∫arceitzz2+1dz|≤πa⋅suparc|eitzz2+1|≤πa⋅suparc1|z2+1|≤πaa2−1,{displaystyle left|int _{mathrm {arc} }{frac {e^{itz}}{z^{2}+1}},dzright|leq pi acdot sup _{text{arc}}left|{frac {e^{itz}}{z^{2}+1}}right|leq pi acdot sup _{text{arc}}{frac {1}{|z^{2}+1|}}leq {frac {pi a}{a^{2}-1}},}{displaystyle left|int _{mathrm {arc} }{frac {e^{itz}}{z^{2}+1}},dzright|leq pi acdot sup _{text{arc}}left|{frac {e^{itz}}{z^{2}+1}}right|leq pi acdot sup _{text{arc}}{frac {1}{|z^{2}+1|}}leq {frac {pi a}{a^{2}-1}},}

and


lima→∞πaa2−1=0.{displaystyle lim _{ato infty }{frac {pi a}{a^{2}-1}}=0.}{displaystyle lim _{ato infty }{frac {pi a}{a^{2}-1}}=0.}

The estimate on the numerator follows since t > 0, and for complex numbers z along the arc (which lies in the upper halfplane), the argument φ of z lies between 0 and π. So,


|eitz|=|eit|z|(cos⁡ϕ+isin⁡ϕ)|=|e−t|z|sin⁡ϕ+it|z|cos⁡ϕ|=e−t|z|sin⁡ϕ≤1.{displaystyle left|e^{itz}right|=left|e^{it|z|(cos phi +isin phi )}right|=left|e^{-t|z|sin phi +it|z|cos phi }right|=e^{-t|z|sin phi }leq 1.}left|e^{itz}right|=left|e^{it|z|(cos phi +isin phi )}right|=left|e^{-t|z|sin phi +it|z|cos phi }right|=e^{-t|z|sin phi }leq 1.

Therefore,


∫−∞∞eitzz2+1dz=πe−t.{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-t}.}{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-t}.}

If t < 0 then a similar argument with an arc C′ that winds around −i rather than i shows that




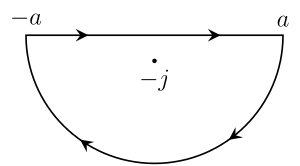
The contour C′.


∫−∞∞eitzz2+1dz=πet,{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{t},}{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{t},}

and finally we have


∫−∞∞eitzz2+1dz=πe−|t|.{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-left|tright|}.}{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-left|tright|}.}

(If t = 0 then the integral yields immediately to elementary calculus methods and its value is π.)



An infinite sum


The fact that π cot(πz) has simple poles with residue 1 at each integer can be used to compute the sum


∑n=−∞∞f(n).{displaystyle displaystyle sum _{n=-infty }^{infty }f(n).}{displaystyle displaystyle sum _{n=-infty }^{infty }f(n).}

Consider, for example, f(z) = z−2. Let ΓN be the rectangle that is the boundary of [−N − 1/2, N + 1/2]2 with positive orientation, with an integer N. By the residue formula,


12πi∫ΓNf(z)πcot⁡(πz)dz=Resz=0+∑n=−Nn≠0Nn−2.{displaystyle {frac {1}{2pi i}}int _{Gamma _{N}}f(z)pi cot(pi z),dz=operatorname {Res} limits _{z=0}+sum _{n=-N atop nneq 0}^{N}n^{-2}.}{displaystyle {frac {1}{2pi i}}int _{Gamma _{N}}f(z)pi cot(pi z),dz=operatorname {Res} limits _{z=0}+sum _{n=-N atop nneq 0}^{N}n^{-2}.}

The left-hand side goes to zero as N → ∞ since the integrand has order O(N−2). On the other hand,[1]


z2cot⁡(z2)=1−B2z22!+⋯;B2=16.{displaystyle {frac {z}{2}}cot left({frac {z}{2}}right)=1-B_{2}{frac {z^{2}}{2!}}+cdots ;qquad B_{2}={frac {1}{6}}.}{displaystyle {frac {z}{2}}cot left({frac {z}{2}}right)=1-B_{2}{frac {z^{2}}{2!}}+cdots ;qquad B_{2}={frac {1}{6}}.}

(In fact, z/2 cot(z/2) = iz/1 − e−iz − iz/2.) Thus, the residue Resz = 0 is −π2/3. We conclude:


∑n=1∞1n2=π26{displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {pi ^{2}}{6}}}{displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {pi ^{2}}{6}}}

which is a proof of the Basel problem.


The same trick can be used to establish


πcot⁡(πz)=limN→∞∑n=−NN(z−n)−1,{displaystyle pi cot(pi z)=lim _{Nto infty }sum _{n=-N}^{N}(z-n)^{-1},}{displaystyle pi cot(pi z)=lim _{Nto infty }sum _{n=-N}^{N}(z-n)^{-1},}

that is, the Eisenstein series.


We take f(z) = (w − z)−1 with w a non-integer and we shall show the above for w. The difficulty in this case is to show the vanishing of the contour integral at infinity. We have:


∫ΓNπcot⁡(πz)zdz=0{displaystyle int _{Gamma _{N}}{frac {pi cot(pi z)}{z}},dz=0}{displaystyle int _{Gamma _{N}}{frac {pi cot(pi z)}{z}},dz=0}

since the integrand is an even function and so the contributions from the contour in the left-half plane and the contour in the right cancel each other out. Thus,


∫ΓNf(z)πcot⁡(πz)dz=∫ΓN(1w−z+1z)πcot⁡(πz)dz{displaystyle int _{Gamma _{N}}f(z)pi cot(pi z),dz=int _{Gamma _{N}}left({frac {1}{w-z}}+{frac {1}{z}}right)pi cot(pi z),dz}{displaystyle int _{Gamma _{N}}f(z)pi cot(pi z),dz=int _{Gamma _{N}}left({frac {1}{w-z}}+{frac {1}{z}}right)pi cot(pi z),dz}

goes to zero as N → ∞.



See also



  • Cauchy's integral formula

  • Glasser's master theorem

  • Jordan's lemma

  • Methods of contour integration

  • Morera's theorem

  • Nachbin's theorem

  • Residue at infinity

  • Logarithmic form



References





  1. ^ Whittaker, E. T.; Watson, G. N. (1902). A Course of Modern Analysis. Cambridge University Press. § 7.2..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}



.mw-parser-output .refbegin{font-size:90%;margin-bottom:0.5em}.mw-parser-output .refbegin-hanging-indents>ul{list-style-type:none;margin-left:0}.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>dd{margin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none}.mw-parser-output .refbegin-100{font-size:100%}



  • Ahlfors, Lars (1979), Complex Analysis, McGraw Hill, ISBN 0-07-085008-9


  • Mitronivić, Dragoslav; Kečkić, Jovan (1984), The Cauchy method of residues: Theory and applications, D. Reidel Publishing Company, ISBN 90-277-1623-4


  • Lindelöf, Ernst (1905), Le calcul des résidus et ses applications à la théorie des fonctions, Editions Jacques Gabay (published 1989), ISBN 2-87647-060-8




External links




  • Hazewinkel, Michiel, ed. (2001) [1994], "Cauchy integral theorem", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4


  • Residue theorem in MathWorld




Comments

Post a Comment

Popular posts from this blog

Information security

Image
This article is part of a series on Information security Related security categories Internet security Cyberwarfare Computer security Mobile security Network security Threats Computer crime Vulnerability Eavesdropping Malware Spyware Ransomware Trojans Viruses Worms Rootkits Bootkits Keyloggers Screen scrapers Exploits Backdoors Logic bombs Payloads Denial of service Defenses Computer access control Application security Antivirus software Secure coding Secure by default Secure by design Secure operating systems Authentication Multi-factor authentication Authorization Data-centric security Encryption Firewall Intrusion detection system Mobile secure gateway Runtime application self-protection (RASP) v t e Information security , sometimes shortened to InfoSec , is the practice of preventing unauthorized access, use, disclosure, disruption, modification, inspection, recording or destruction of information. Th...
Read more

Volkswagen Group MQB platform

Image
The Volkswagen Group MQB platform is the company's strategy for shared modular design construction of its transverse, front-engine, front-wheel-drive layout (optional front-engine, four-wheel-drive layout) automobiles. Volkswagen spent roughly $60bn [1] developing this new platform and the cars employing it. The platform underpins a wide range of cars from the supermini class to the mid size SUV class. MQB allows Volkswagen to assemble any of its cars based on this platform across all of its MQB ready factories. This allows the Volkswagen group flexibility to shift production as needed between its different factories. Beginning in 2012, Volkswagen Group marketed the strategy under the code name MQB , which stands for Modularer Querbaukasten , translating from German to "Modular Transversal Toolkit" or "Modular Transverse Matrix". [2] [3] MQB is one strategy within VW's overall MB (Modularer Baukasten or modular matrix) program which also includes th...
Read more

刘萌萌

Image
body.skin-minerva .mw-parser-output table.infobox caption{text-align:center} 刘萌萌 女演员 罗马拼音 Liu Meng Meng 英文名 Cya 国籍   中国 民族 汉族 出生 ( 1989-10-16 ) 1989年10月16日 （ 29歲）   中国辽宁省大连市 职业 演员、艺人 语言 汉语 教育程度 沈阳音乐学院 北京电影学院表演系进修班 活跃年代 2011年至今 唱片公司 浙江永乐影视制作有限公司 经纪公司 浙江永乐影视制作有限公司 网站 刘萌萌 官方微博 刘萌萌 （1989年10月16日 － ），汉族，中国演员，2010年参加湖南卫视《芒果训练营》而出道至今，凭借电视剧《爱情公寓》“诺澜”一角走红。北京电影学院10级表演系（进修班）毕业。 目录 1 主要经历 2 影视作品 2.1 电视剧 2.2 电影 2.3 综艺节目 3 参考文献 4 外部链接 主要经历 1989年，出生于辽宁省大连市一个工人家庭； 2006年，考入沈阳音乐学院舞蹈系本科班学习； 2010年，参加湖南卫视《芒果训练营》演艺新秀比赛而出道 [1] ；進入北京电影学院表演系进修班 2011年，出演电视剧《隋唐演义》“琼花公主”一角色； 2012年，担任电视剧《爱情公寓》“诺澜”一角并开始走红 [2] ； 2013年，担任电视剧《利箭纵横》《利剑行动》 [3] 女主角“林筱雨” 2014年，参加江苏卫视真人秀栏目《花样年华》 [4] 备受瞩目 [5] 。 影视作品 电视剧 首播年份 剧名 角色 备注 2012 《爱情公寓3》 诺澜 2012 《利箭行动》 林筱雨 2013 《隋唐演义》 琼花公主 2013 《决战燕子门》 马晓婉 2014 《利箭纵横》 林筱雨 2014 《屌丝日记》 林洛霏 網絡劇 2014 《爱情公寓4》 诺澜 ...
Read more