Mixing
正交幅度调制
| 调制方式 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 連續調變 | |||||||||||||||
| |||||||||||||||
| 脈衝调制 | |||||||||||||||
| 模拟 | PAM · PDM · PPM |
||||||||||||||
| 数字 | PCM · PWM |
||||||||||||||
| 扩频 | |||||||||||||||
CSS · DSSS · THSS · FHSS | |||||||||||||||
| 另見 | |||||||||||||||
调制 · 线路码 · 调制解调器 · ΔΣ調變 · OFDM · FDM | |||||||||||||||
正交幅度调制（QAM，Quadrature Amplitude Modulation）是一种在两个正交载波上进行幅度调制的调制方式。这两个载波通常是相位差为90度（π/2）的正弦波，因此被称作正交载波。这种调制方式因此而得名。
目录
1 概述
2 性能
3 矩形QAM
3.1 误码率性能
4 非矩形QAM
5 星座图表示
6 优缺点
7 参见
概述
同其它调制方式类似，QAM通过载波某些参数的变化传输信息。在QAM中，数据信号由相互正交的两个载波的幅度变化表示。
模拟信号的相位调制和数字信号的PSK可以被认为是幅度不变、仅有相位变化的特殊的正交幅度调制。由此，模拟信号频率调制和数字信号FSK也可以被认为是相位调制（PSK）的特例，因为它们本质上就是相位调制。这里主要讨论数字信号的QAM，虽然模拟信号QAM也有很多应用，例如NTSC和PAL制式的电视系统就利用正交的载波传输不同的颜色分量。
类似于其他数字调制方式，QAM发射信号集可以用星座图方便地表示。星座图上每一个星座点对应发射信号集中的一个信号。设正交幅度调制的发射信号集大小为N{displaystyle N}
当对数据传输速率的要求高过8-PSK能提供的上限时，一般采用QAM的调制方式。因为QAM的星座点比PSK的星座点更分散，星座点之间的距离因之更大，所以能提供更好的传输性能。但是QAM星座点的幅度不是完全相同的，所以它的解调器需要能同时正确检测相位和幅度，不像PSK解调只需要检测相位，这增加了QAM解调器的复杂性。
M-QAM信号波形的表达式为：
- sm(t)=ℜ[(Amc+jAms)g(t)ej2πfct]=Amcg(t)cos2πfct−Amsg(t)sin2πfct ,where m=1,2,…,M{displaystyle s_{m}(t)=Re [(A_{mc}+jA_{ms})g(t)e^{j2pi f_{c}t}]=A_{mc}g(t)cos 2pi f_{c}t-A_{ms}g(t)sin 2pi f_{c}t{mbox{ ,where }}m=1,2,ldots ,M}
- 其中g(t){displaystyle g(t)}
为码元信号脉冲。
![s_{m}(t)=Re [(A_{{mc}}+jA_{{ms}})g(t)e^{{j2pi f_{c}t}}]=A_{{mc}}g(t)cos 2pi f_{c}t-A_{{ms}}g(t)sin 2pi f_{c}t{mbox{ ,where }}m=1,2,ldots ,M](https://wikimedia.org/api/rest_v1/media/math/render/svg/d19aba03080c3cb4ddee9b49bdafe93f2d8a1fbc)
因此QAM可以分解为分别在两个正交的载波cos2πfct{displaystyle cos 2pi f_{c}t}
将上面sm(t){displaystyle s_{m}(t)}
- sm(t)=ℜ[Vmejθmg(t)ej2πfct]=Vmg(t)cos(2πfct+θm){displaystyle s_{m}(t)=Re [V_{m}e^{jtheta m}g(t)e^{j2pi f_{c}t}]=V_{m}g(t)cos(2pi f_{c}t+theta _{m})}
- 其中Vm=Amc2+Ams2{displaystyle V_{m}={sqrt {A_{mc}^{2}+A_{ms}^{2}}}}
，θm=arctan(Ams/Amc){displaystyle theta _{m}=arctan(A_{ms}/A_{mc})}
。
![s_{m}(t)=Re [V_{m}e^{{jtheta m}}g(t)e^{{j2pi f_{c}t}}]=V_{m}g(t)cos(2pi f_{c}t+theta _{m})](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba86369fc7f0031d73933c01a842fb26ab1a7038)
因此，M-QAM还可以看作是M1-PAM与M2-PSK的叠加，其中M1M2=M{displaystyle M_{1}M_{2}=M}
性能
数字通信中经常用错误率（包括误符号率和误比特率）与信噪比的关系衡量调制和解调方式的性能。下面给出一些概念的记法，以得到AWGN信道下错误率的表达式：
M{displaystyle M}= 星座点的个数
Eb{displaystyle E_{b}}= 平均比特能量
Es{displaystyle E_{s}}= 平均符号能量 = Eb⋅log2M{displaystyle E_{b}cdot log _{2}{M}}
N0{displaystyle N_{0}}= 噪声功率谱密度
Pb{displaystyle P_{b}}= 误比特率
Pbc{displaystyle P_{bc}}= 每个正交载波上的误比特率
Ps{displaystyle P_{s}}= 误符号率
Psc{displaystyle P_{sc}}= 每个正交载波上的误符号率
- Q(x)=12π∫x∞e−t2/2dt=12erfc(x2), x≥0{displaystyle Q(x)={frac {1}{sqrt {2pi }}}int _{x}^{infty }e^{-t^{2}/2}dt={frac {1}{2}}operatorname {erfc} left({frac {x}{sqrt {2}}}right), xgeq {}0}
Q(x){displaystyle Q(x)}表示有着零均值和单位方差的高斯随机变量t 大于x的概率。它与高斯误差补函数的关系是：Q(x)=12erfc(x2){displaystyle Q(x)={frac {1}{2}}operatorname {erfc} left({frac {x}{sqrt {2}}}right)}
。
矩形QAM
矩形QAM（Rectangular QAM）的星座图呈矩形网格配置。因为矩形QAM信号之间的最小距离并不是相同能量下最大的，因此它的误码率性能没有达到最优。不过，考虑到矩形QAM等效于两个正交载波上的脉冲幅度调制（PAM）的叠加，因此矩形QAM的调制解调比较简单。而后面介绍的非矩形QAM虽然能达到略好一些的误码率性能，但是付出的代价是困难得多的调制和解调。
最早的矩形QAM一般是16-QAM。其原因是很容易就看得出来2-QAM和4-QAM实际上是二进制相移键控（BPSK）和正交相移键控（QPSK），而8-QAM则有将单数位的位分到两个载波上的问题，8-PSK要容易得多，因此8-QAM很少被使用。
误码率性能
- 对于偶数-k{displaystyle k}
QAM的误码率性能
可以通过单个正交载波上PAM的性能近似得到QAM的误码率。假设矩形M{displaystyle M}
Psc=PM-PAM=2(1−1M)Q(3M−1EsN0){displaystyle P_{sc}=P_{{sqrt {M}}{mbox{-PAM}}}=2left(1-{frac {1}{sqrt {M}}}right)Qleft({sqrt {{frac {3}{M-1}}{frac {E_{s}}{N_{0}}}}}right)},
因此
Ps=1−(1−Psc)2{displaystyle ,P_{s}=1-left(1-P_{sc}right)^{2}}.
精确的误比特率要看比特与码元符号之间的映射关系。对于以格雷码作bit配置并且每个载波承载相同比特数的情况，由于相邻两个符号之间仅相差一个比特，因此可以得到误比特率：
Pbc=4k(1−1M)Q(3kM−1EbN0){displaystyle P_{bc}={frac {4}{k}}left(1-{frac {1}{sqrt {M}}}right)Qleft({sqrt {{frac {3k}{M-1}}{frac {E_{b}}{N_{0}}}}}right)},
由于子载波相互独立，所以：
- Pb=Pbc{displaystyle P_{b}=P_{bc}}
- 对于奇数-k{displaystyle k}
对于k{displaystyle k}
Ps≤4Q(3kEb(M−1)N0){displaystyle P_{s}leq {}4Qleft({sqrt {frac {3kE_{b}}{(M-1)N_{0}}}}right)}.
精确的误比特率Pb{displaystyle P_{b}}
非矩形QAM
QAM本身有许多可以使用的排列，这里只列出两种为例。
环状8-QAM是最佳的8-QAM，它可以使用最低的平均能量来达到最小的欧几里得度量。环状的16-QAM是亚优化的。环状的QAM非常好地显示出QAM与PSK之间的关系。不规则QAM的错误率很难广泛地给出，因为它们按其排列各不相同。显然的上限是欧几里得度量：
Ps<(M−1)Q(dmin2/2N0){displaystyle P_{s}<(M-1)Qleft({sqrt {d_{min}^{2}/2N_{0}}}right)}.
在这里误码率也与位的排列有关。
虽然对一个特别的M{displaystyle M}
星座图表示
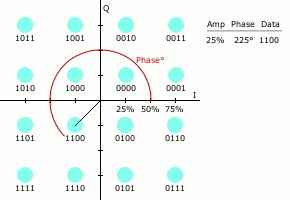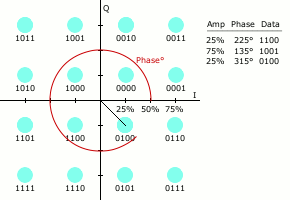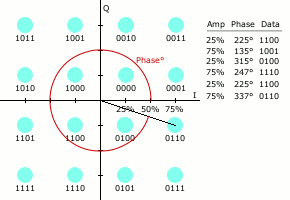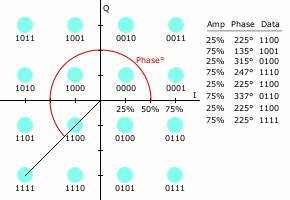
类似于其他数字调制方式，QAM发射的信号集可以用星座图方便地表示，星座图上每一个星座点对应发射信号集中的那一点。
星座点经常采用水平和垂直方向等间距的正方网格配置，当然也有其他的配置方式。
数字通信中数据常采用二进制数表示，这种情况下星座点的个数一般是2的幂。
星座点数越多，每个符号能传输的信息量就越大。但是，如果在星座图的平均能量保持不变的情况下增加星座点，会使星座点之间的距离变小，进而导致误码率上升。因此高阶星座图的可靠性比低阶要差。
采用QAM调制技术，信道带宽至少要等于码元速率，为了定时恢复，还需要另外的带宽，一般要增加15%左右。
优缺点
与其他调制技术相比，QAM编码具有能充分利用带宽、抗噪声能力强等优点。
但QAM调制技术用于ADSL的主要问题是如何适应不同电话线路之间较大的性能差异。要取得较为理想的工作特性，QAM接收器需要一个和发送端具有相同的频谱和相应特性的输入信号用于解码，QAM接收器利用自适应均衡器来补偿传输过程中信号产生的失真，因此采用QAM的 ADSL系统的复杂性来自于它的自适应均衡器。
当对数据传输速率的要求高过8-PSK能提供的上限时，一般采用QAM的调制方式。因为QAM的星座点比PSK的星座点更分散，星座点之间的距离因此更大，所以能提供更好的传输性能。
但是QAM星座点的幅度不是完全相同的，所以它的解调器需要能同时正确检测相位和幅度，不像PSK解调只需要检测相位，这增加了QAM解调器的复杂性。
参见
- 调制
- 相位偏移調變
- 頻率偏移調變
Comments
Post a Comment