Lambert W function

Multivalued "function"

The graph of W(x) for W > −4 and x < 6. The upper branch with W ≥ −1 is the function W₀ (principal branch), the lower branch with W ≤ −1 is the function W₋₁.

In mathematics, the Lambert W function, also called the omega function or product logarithm, is a set of functions, namely the branches of the inverse relation of the function f(z) = ze^z, where e^z is the exponential function, and z is any complex number. In other words

z=f−1(zez)=W(zez).{displaystyle z=f^{-1}left(ze^{z}right)=Wleft(ze^{z}right).}

By substituting z₀ = ze^z into the equation above, we get the defining equation for the W function (and for the W relation in general):

z0=W(z0)eW(z0){displaystyle z_{0}=W(z_{0})e^{W(z_{0})}}

for any complex number z₀.

Since the function f is not injective, the relation W is multivalued (except at 0). If we restrict attention to real-valued W, the complex variable z is then replaced by the real variable x, and the relation is defined only for x ≥ −1/e and is double-valued on (−1/e, 0). The additional constraint W ≥ −1 defines a single-valued function W₀(x). We have W₀(0) = 0 and W₀(−1/e) = −1. Meanwhile, the lower branch has W ≤ −1 and is denoted W₋₁(x). It decreases from W₋₁(−1/e) = −1 to W₋₁(0⁻) = −∞.

It can be extended to the function z = xa^x using the identity

x=W(zln⁡a)ln⁡a.{displaystyle x={frac {W(zln {a})}{ln {a}}}.}

The Lambert W relation cannot be expressed in terms of elementary functions.^[1] It is useful in combinatorics, for instance, in the enumeration of trees. It can be used to solve various equations involving exponentials (e.g. the maxima of the Planck, Bose–Einstein, and Fermi–Dirac distributions) and also occurs in the solution of delay differential equations, such as y′(t) = a y(t − 1). In biochemistry, and in particular enzyme kinetics, a closed-form solution for the time-course kinetics analysis of Michaelis–Menten kinetics is described in terms of the Lambert W function.

Main branch of the Lambert W function in the complex plane. Note the branch cut along the negative real axis, ending at −1/e. In this picture, the hue of a point z is determined by the argument of W(z), and the brightness by the absolute value of W(z).

The modulus of the principal branch of the Lambert W function, colored according to arg W(z)

Contents

• 
  1 Terminology
  


• 
  2 History
  


• 
  3 Calculus
  
  
  
  • 
    3.1 Derivative
    
  
  
  • 
    3.2 Antiderivative
    
  
  
  
  


• 
  4 Asymptotic expansions
  
  
  
  • 
    4.1 Integer and complex powers
    
  
  
  
  


• 
  5 Identities
  


• 
  6 Special values
  


• 
  7 Representations
  


• 
  8 Branches and range
  


• 
  9 Other formulas
  
  
  
  • 
    9.1 Definite integrals
    
  
  
  • 
    9.2 Indefinite integrals
    
  
  
  
  


• 
  10 Solutions of equations
  
  
  
  • 
    10.1 Example 1
    
  
  
  • 
    10.2 Example 2
    
  
  
  • 
    10.3 Example 3
    
  
  
  • 
    10.4 Example 4
    
  
  
  • 
    10.5 Example 5
    
  
  
  • 
    10.6 Example 6
    
  
  
  • 
    10.7 Example 7
    
  
  
  
  


• 
  11 Applications
  
  
  
  • 
    11.1 Instrument design
    
  
  
  • 
    11.2 Viscous flows
    
  
  
  • 
    11.3 Neuroimaging
    
  
  
  • 
    11.4 Chemical engineering
    
  
  
  • 
    11.5 Materials science
    
  
  
  • 
    11.6 Porous media
    
  
  
  • 
    11.7 Bernoulli numbers and Todd genus
    
  
  
  • 
    11.8 Statistics
    
  
  
  • 
    11.9 Exact solutions of the Schrödinger equation
    
  
  
  • 
    11.10 Exact solutions of the Einstein vacuum equations
    
  
  
  • 
    11.11 Resonances of the delta-shell potential
    
  
  
  • 
    11.12 Thermodynamic equilibrium
    
  
  
  • 
    11.13 AdS/CFT correspondence
    
  
  
  
  


• 
  12 Generalizations
  


• 
  13 Plots
  


• 
  14 Numerical evaluation
  


• 
  15 Software
  


• 
  16 See also
  


• 
  17 Notes
  


• 
  18 References
  


• 
  19 External links
  

Terminology

The two main branches W₀ and W₋₁.

The Lambert W function is named after Johann Heinrich Lambert. The main branch W₀ is denoted Wp in the Digital Library of Mathematical Functions, and the branch W₋₁ is denoted Wm there.

The notation convention chosen here (with W₀ and W₋₁) follows the canonical reference on the Lambert W function by Corless, Gonnet, Hare, Jeffrey and Knuth.^[2]

History

Lambert first considered the related Lambert's Transcendental Equation in 1758,^[3] which led to an article by Leonhard Euler in 1783^[4] that discussed the special case of we^w.

The function Lambert considered was

x=xm+q.{displaystyle x=x^{m}+q.}

Euler transformed this equation into the form

xa−xb=(a−b)cxa+b.{displaystyle x^{a}-x^{b}=(a-b)cx^{a+b}.}

Both authors derived a series solution for their equations.

Once Euler had solved this equation he considered the case a = b. Taking limits he derived the equation

ln⁡x=cxa.{displaystyle ln x=cx^{a}.}

He then put a = 1 and obtained a convergent series solution.

After taking derivatives with respect to x and some manipulation, the standard form of the Lambert function is obtained.

In 1993, when it was reported that the Lambert W function provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in physics—Corless and developers of the Maple computer algebra system made a library search and found that this function was ubiquitous in nature.^[2][5]

Another example where this function is found is in Michaelis–Menten kinetics.

Calculus

Derivative

By implicit differentiation, one can show that all branches of W satisfy the differential equation

z(1+W)dWdz=Wfor z≠−1e.{displaystyle z(1+W){frac {dW}{dz}}=Wquad {text{for }}zneq -{frac {1}{e}}.}

(W is not differentiable for z = −1/e.) As a consequence, we get the following formula for the derivative of W:

dWdz=W(z)z(1+W(z))for z∉{0,−1e}.{displaystyle {frac {dW}{dz}}={frac {W(z)}{z(1+W(z))}}quad {text{for }}znot in left{0,-{frac {1}{e}}right}.}

Using the identity e^W(z) = z / W(z), we get the following equivalent formula:

dWdz=1z+eW(z)for z≠−1e.{displaystyle {frac {dW}{dz}}={frac {1}{z+e^{W(z)}}}quad {text{for }}zneq -{frac {1}{e}}.}

Antiderivative

The function W(x), and many expressions involving W(x), can be integrated using the substitution w = W(x), i.e. x = we^w:

∫W(x)dx=xW(x)−x+eW(x)+C=x(W(x)−1+1W(x))+C.{displaystyle {begin{aligned}int W(x),dx&=xW(x)-x+e^{W(x)}+C\&=xleft(W(x)-1+{frac {1}{W(x)}}right)+C.end{aligned}}}

(The last equation is more common in the literature but does not hold at x = 0). One consequence of this (using the fact that W(e) = 1) is the identity

∫0eW(x)dx=e−1.{displaystyle int _{0}^{e}W(x),dx=e-1.}

Asymptotic expansions

The Taylor series of W₀ around 0 can be found using the Lagrange inversion theorem and is given by

W0(x)=∑n=1∞(−n)n−1n!xn=x−x2+32x3−83x4+12524x5−⋯.{displaystyle W_{0}(x)=sum _{n=1}^{infty }{frac {(-n)^{n-1}}{n!}}x^{n}=x-x^{2}+{tfrac {3}{2}}x^{3}-{tfrac {8}{3}}x^{4}+{tfrac {125}{24}}x^{5}-cdots .}

The radius of convergence is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function defined on all complex numbers with a branch cut along the interval (−∞, −1/e]; this holomorphic function defines the principal branch of the Lambert W function.

For large values of x, W₀ is asymptotic to

W0(x)=L1−L2+L2L1+L2(−2+L2)2L12+L2(6−9L2+2L22)6L13+L2(−12+36L2−22L22+3L23)12L14+⋯=L1−L2+∑l=0∞∑m=1∞(−1)l[l+ml+1]m!L1−l−mL2m,{displaystyle {begin{aligned}W_{0}(x)&=L_{1}-L_{2}+{frac {L_{2}}{L_{1}}}+{frac {L_{2}left(-2+L_{2}right)}{2L_{1}^{2}}}+{frac {L_{2}left(6-9L_{2}+2L_{2}^{2}right)}{6L_{1}^{3}}}+{frac {L_{2}left(-12+36L_{2}-22L_{2}^{2}+3L_{2}^{3}right)}{12L_{1}^{4}}}+cdots \[5pt]&=L_{1}-L_{2}+sum _{l=0}^{infty }sum _{m=1}^{infty }{frac {(-1)^{l}left[{begin{smallmatrix}l+m\l+1end{smallmatrix}}right]}{m!}}L_{1}^{-l-m}L_{2}^{m},end{aligned}}}

where L₁ = ln x, L₂ = ln ln x, and [^{l + m}
_{l + 1}] is a non-negative Stirling number of the first kind.^[2] Keeping only the first two terms of the expansion,

W0(x)=ln⁡x−ln⁡ln⁡x+o(1).{displaystyle W_{0}(x)=ln x-ln ln x+o(1).}

The other real branch, W₋₁, defined in the interval [−1/e, 0), has an approximation of the same form as x approaches zero, with in this case L₁ = ln(−x) and L₂ = ln(−ln(−x)).^[2]

It is shown^[6] that the following bound holds for x ≥ e:

ln⁡x−ln⁡ln⁡x+ln⁡ln⁡x2ln⁡x≤W0(x)≤ln⁡x−ln⁡ln⁡x+ee−1ln⁡ln⁡xln⁡x.{displaystyle ln x-ln ln x+{frac {ln ln x}{2ln x}}leq W_{0}(x)leq ln x-ln ln x+{frac {e}{e-1}}{frac {ln ln x}{ln x}}.}

In 2016 it was proven^[7] that the branch W₋₁ can be bounded as follows:

−1−2u−u<W−1(−e−u−1)<−1−2u−23ufor u>0.{displaystyle -1-{sqrt {2u}}-u<W_{-1}left(-e^{-u-1}right)<-1-{sqrt {2u}}-{tfrac {2}{3}}uquad {text{for }}u>0.}

Integer and complex powers

Integer powers of W₀ also admit simple Taylor (or Laurent) series expansions at zero:

W0(x)2=∑n=2∞−2(−n)n−3(n−2)!xn=x2−2x3+4x4−253x5+18x6−⋯.{displaystyle W_{0}(x)^{2}=sum _{n=2}^{infty }{frac {-2left(-nright)^{n-3}}{(n-2)!}}x^{n}=x^{2}-2x^{3}+4x^{4}-{tfrac {25}{3}}x^{5}+18x^{6}-cdots .}

More generally, for r ∈ ℤ, the Lagrange inversion formula gives

W0(x)r=∑n=r∞−r(−n)n−r−1(n−r)!xn,{displaystyle W_{0}(x)^{r}=sum _{n=r}^{infty }{frac {-rleft(-nright)^{n-r-1}}{(n-r)!}}x^{n},}

which is, in general, a Laurent series of order r. Equivalently, the latter can be written in the form of a Taylor expansion of powers of W₀(x) / x:

(W0(x)x)r=e−rW0(x)=∑n=0∞r(n+r)n−1n!(−x)n,{displaystyle left({frac {W_{0}(x)}{x}}right)^{r}=e^{-rW_{0}(x)}=sum _{n=0}^{infty }{frac {rleft(n+rright)^{n-1}}{n!}}left(-xright)^{n},}

which holds for any r ∈ ℂ and |x| < 1/e.

Identities

A few identities follow from the definition:

W(xex)=xfor x≥0,W0(xex)=xfor x≥−1,W−1(xex)=xfor x≤−1.{displaystyle {begin{aligned}W(xe^{x})&=x&{text{for }}x&geq 0,\W_{0}(xe^{x})&=x&{text{for }}x&geq -1,\W_{-1}(xe^{x})&=x&{text{for }}x&leq -1.end{aligned}}}

Note that, since f(x) = xe^x is not injective, it does not always hold that W(f(x)) = x, much like with the inverse trigonometric functions. For fixed x < 0 and x ≠ −1, the equation xe^x = ye^y has two solutions in y, one of which is of course y = x. Then, for i = 0 and x < −1, as well as for i = −1 and x ∈ (−1, 0), y = W_i(xe^x) is the other solution.

Some other identities:^[8]

W(x)⋅eW(x)=x,therefore:eW(x)=xW(x),e−W(x)=W(x)x,enW(x)=(xW(x))n.{displaystyle {begin{aligned}&W(x)cdot e^{W(x)}=x,quad {text{therefore:}}\[5pt]&e^{W(x)}={frac {x}{W(x)}},qquad e^{-W(x)}={frac {W(x)}{x}},qquad e^{nW(x)}=left({frac {x}{W(x)}}right)^{n}.end{aligned}}}

ln⁡W(x)=ln⁡x−W(x)for x>0.{displaystyle ln W(x)=ln x-W(x)quad {text{for }}x>0.}^[9]

W(aln⁡a)=ln⁡afor a∈R.{displaystyle Wleft(aln aright)=ln aquad {text{for }}ain mathbb {R} .}

W(x)=ln⁡xW(x)for x≥−1e,W(nxnW(x)n−1)=nW(x)for n,x>0{displaystyle {begin{aligned}&W(x)=ln {frac {x}{W(x)}}&&{text{for }}xgeq -{frac {1}{e}},\[5pt]&Wleft({frac {nx^{n}}{Wleft(xright)^{n-1}}}right)=nW(x)&&{text{for }}n,x>0end{aligned}}}

(which can be extended to other n and x if the right branch is chosen).

W(x)+W(y)=W(xy(1W(x)+1W(y)))for x,y>0.{displaystyle W(x)+W(y)=Wleft(xyleft({frac {1}{W(x)}}+{frac {1}{W(y)}}right)right)quad {text{for }}x,y>0.}

From inverting f(ln x):

W(xln⁡x)=ln⁡x=W(x)+ln⁡W(x)for x>0.{displaystyle {begin{aligned}W(xln x)&=ln x\&=W(x)+ln W(x)quad {text{for }}x>0.end{aligned}}}

Substituting −ln x in the definition:

W0(−ln⁡xx)=−ln⁡xfor 0<x≤e,W−1(−ln⁡xx)=−ln⁡xfor x>e.{displaystyle {begin{aligned}W_{0}left(-{frac {ln x}{x}}right)&=-ln x&{text{for }}0&<xleq e,\[5pt]W_{-1}left(-{frac {ln x}{x}}right)&=-ln x&{text{for }}x&>e.end{aligned}}}

With Euler's iterated exponential h(x):

h(x)=e−W(−ln⁡x)=W(−ln⁡x)−ln⁡xfor x≠1.{displaystyle {begin{aligned}h(x)&=e^{-W(-ln x)}\&={frac {W(-ln x)}{-ln x}}quad {text{for }}xneq 1.end{aligned}}}

Special values

For any nonzero algebraic number x, W(x) is a transcendental number. Indeed, if W(x) is zero, then x must be zero as well, and if W(x) is nonzero and algebraic, then by the Lindemann–Weierstrass theorem, e^W(x) must be transcendental, implying that x = W(x)e^W(x) must also be transcendental.

W(−π2)=iπ2.{displaystyle Wleft(-{frac {pi }{2}}right)={frac {ipi }{2}}.}

W(−1e)=−1.{displaystyle Wleft(-{frac {1}{e}}right)=-1.}

W(−ln⁡aa)=−ln⁡a(1e≤a≤e).{displaystyle Wleft(-{frac {ln a}{a}}right)=-ln aquad left({frac {1}{e}}leq aleq eright).}

W(2ln⁡2)=ln⁡2.{displaystyle Wleft(2ln 2right)=ln 2.}

W(0)=0.{displaystyle W(0)=0.}

W(1)=Ω=(∫−∞∞dt(et−t)2+π2)−1−1≈0.56714329…{displaystyle W(1)=Omega =left(int _{-infty }^{infty }{frac {dt}{left(e^{t}-tright)^{2}+pi ^{2}}}right)^{-1}-1approx 0.56714329ldots } (the Omega constant).

W(1)=e−W(1)=ln⁡(1W(1))=−ln⁡W(1).{displaystyle W(1)=e^{-W(1)}=ln left({frac {1}{W(1)}}right)=-ln W(1).}

W(e)=1.{displaystyle W(e)=1.}

W(e1+e)=e.{displaystyle W(e^{1+e})=e.}

W(−1)≈−0.31813+1.33723i.{displaystyle W(-1)approx -0.31813+1.33723i.}

W′(0)=1.{displaystyle W'(0)=1.}

Representations

The principal branch of the Lambert function can be represented by a proper integral, due to Poisson:^[10]

−π2W(−x)=∫0πsin⁡(32t)−xecos⁡tsin⁡(52t−sin⁡t)1−2xecos⁡tcos⁡(t−sin⁡t)+x2e2cos⁡tsin⁡(12t)dtfor |x|<1e.{displaystyle -{frac {pi }{2}}W(-x)=int _{0}^{pi }{frac {sin left({tfrac {3}{2}}tright)-xe^{cos t}sin left({tfrac {5}{2}}t-sin tright)}{1-2xe^{cos t}cos(t-sin t)+x^{2}e^{2cos t}}}sin left({tfrac {1}{2}}tright),dtquad {text{for }}|x|<{frac {1}{e}}.}

On the wider domain −1/e ≤ x ≤ e, the considerably simpler representation is found by Mező:^[11]

W(x)=1πRe⁡∫0πln⁡(eeit−xe−iteeit−xeit)dt.{displaystyle W(x)={frac {1}{pi }}operatorname {Re} int _{0}^{pi }ln left({frac {e^{e^{it}}-xe^{-it}}{e^{e^{it}}-xe^{it}}}right),dt.}

The following continued fraction representation also holds for the principal branch:^[12]

W(x)=x1+x1+x2+5x3+17x10+133x17+1927x190+13582711x94423+⋱.{displaystyle W(x)={cfrac {x}{1+{cfrac {x}{1+{cfrac {x}{2+{cfrac {5x}{3+{cfrac {17x}{10+{cfrac {133x}{17+{cfrac {1927x}{190+{cfrac {13582711x}{94423+ddots }}}}}}}}}}}}}}}}.}

Also, if |W(z)| < 1:^[13]

W(x)=xexp⁡xexp⁡x⋱.{displaystyle W(x)={cfrac {x}{exp {cfrac {x}{exp {cfrac {x}{ddots }}}}}}.}

In turn, if |W(z)| > 1, then

W(x)=ln⁡xln⁡xln⁡x⋱.{displaystyle W(x)=ln {cfrac {x}{ln {cfrac {x}{ln {cfrac {x}{ddots }}}}}}.}

Branches and range

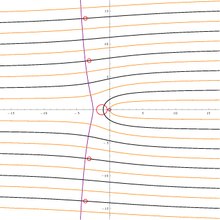
The range of the W function, showing all branches. The orange curves are the images of the imaginary axis. The black are the images of the real axis (the quadratrix of Hippias). The purple curves is the image of a small circle around the branch point z = 0; the red curves are the images of a small circle around the point z = −1/e.

There are countably many branches of the W function, denoted by W_k(z), for integer k; W₀(z) being the principal branch. The branch point for the principal branch is at z = −1/e, with a branch cut that extends to −∞ along the negative real axis. This branch cut separates the principal branch from the two branches W₋₁ and W₁. In all other branches, there is a branch point at z = 0 and a branch cut along the whole negative real axis.

The range of the entire function is the complex plane. The image of the real axis coincides with the quadratrix of Hippias, the parametric curve w = −t cot t + it.

Other formulas

Definite integrals

There are several useful definite integral formulas involving the W function, including the following:

∫0πW(2cot2⁡x)sec2⁡xdx=4π.∫0∞W(x)xxdx=22π.∫0∞W(1x2)dx=2π.{displaystyle {begin{aligned}&int _{0}^{pi }Wleft(2cot ^{2}xright)sec ^{2}x,dx=4{sqrt {pi }}.\[5pt]&int _{0}^{infty }{frac {W(x)}{x{sqrt {x}}}},dx=2{sqrt {2pi }}.\[5pt]&int _{0}^{infty }Wleft({frac {1}{x^{2}}}right),dx={sqrt {2pi }}.end{aligned}}}

The first identity can be found by writing the Gaussian integral in polar coordinates.

The second identity can be derived by making the substitution u = W(x), which gives

x=ueu,dxdu=(u+1)eu.{displaystyle {begin{aligned}x&=ue^{u},\[5pt]{frac {dx}{du}}&=(u+1)e^{u}.end{aligned}}}

Thus

∫0∞W(x)xxdx=∫0∞uueuueu(u+1)eudu=∫0∞u+1ueudu=∫0∞u+1u1eudu=∫0∞u12e−u2du+∫0∞u−12e−u2du=2∫0∞(2w)12e−wdw+2∫0∞(2w)−12e−wdw(u=2w)=22∫0∞w12e−wdw+2∫0∞w−12e−wdw=22⋅Γ(32)+2⋅Γ(12)=22(12π)+2(π)=22π.{displaystyle {begin{aligned}int _{0}^{infty }{frac {W(x)}{x{sqrt {x}}}},dx&=int _{0}^{infty }{frac {u}{ue^{u}{sqrt {ue^{u}}}}}(u+1)e^{u},du\[5pt]&=int _{0}^{infty }{frac {u+1}{sqrt {ue^{u}}}}du\[5pt]&=int _{0}^{infty }{frac {u+1}{sqrt {u}}}{frac {1}{sqrt {e^{u}}}}du\[5pt]&=int _{0}^{infty }u^{tfrac {1}{2}}e^{-{frac {u}{2}}}du+int _{0}^{infty }u^{-{tfrac {1}{2}}}e^{-{frac {u}{2}}}du\[5pt]&=2int _{0}^{infty }(2w)^{tfrac {1}{2}}e^{-w},dw+2int _{0}^{infty }(2w)^{-{tfrac {1}{2}}}e^{-w},dw&&quad (u=2w)\[5pt]&=2{sqrt {2}}int _{0}^{infty }w^{tfrac {1}{2}}e^{-w},dw+{sqrt {2}}int _{0}^{infty }w^{-{tfrac {1}{2}}}e^{-w},dw\[5pt]&=2{sqrt {2}}cdot Gamma left({tfrac {3}{2}}right)+{sqrt {2}}cdot Gamma left({tfrac {1}{2}}right)\[5pt]&=2{sqrt {2}}left({tfrac {1}{2}}{sqrt {pi }}right)+{sqrt {2}}left({sqrt {pi }}right)\[5pt]&=2{sqrt {2pi }}.end{aligned}}}

The third identity may be derived from the second by making the substitution u = x⁻² and the first can also be derived from the third by the substitution z = (tan x) / √2.

Except for z along the branch cut (−∞, −1/e] (where the integral does not converge), the principal branch of the Lambert W function can be computed by the following integral:^[14]

W(z)=z2π∫−ππ(1−νcot⁡ν)2+ν2z+νcsc⁡νe−νcot⁡νdν=zπ∫0π(1−νcot⁡ν)2+ν2z+νcsc⁡νe−νcot⁡νdν,{displaystyle {begin{aligned}W(z)&={frac {z}{2pi }}int _{-pi }^{pi }{frac {left(1-nu cot nu right)^{2}+nu ^{2}}{z+nu csc nu e^{-nu cot nu }}},dnu \[5pt]&={frac {z}{pi }}int _{0}^{pi }{frac {left(1-nu cot nu right)^{2}+nu ^{2}}{z+nu csc nu e^{-nu cot nu }}},dnu ,end{aligned}}}

where the two integral expressions are equivalent due to the symmetry of the integrand.

Indefinite integrals

∫W(x)xdx=12(1+W(x))2+C.∫W(AeBx)dx=12B(1+W(AeBx))2+C.{displaystyle {begin{aligned}&int {frac {W(x)}{x}}dx={tfrac {1}{2}}left(1+W(x)right)^{2}+C.\[5pt]&int Wleft(Ae^{Bx}right)dx={frac {1}{2B}}left(1+Wleft(Ae^{Bx}right)right)^{2}+C.end{aligned}}}

Solutions of equations

Many equations involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like Y = Xe^X at which point the W function provides the value of the variable in X. In other words:

Y=XeX⟺X=W(Y).{displaystyle Y=Xe^{X};Longleftrightarrow ;X=W(Y).}

Example 1

2t=5t1=5t2t1=5te−tln⁡215=te−tln⁡2−ln⁡25=(−tln⁡2)e−tln⁡2W(−ln⁡25)=−tln⁡2t=−W(−ln⁡25)ln⁡2.{displaystyle {begin{aligned}2^{t}&=5t\[5pt]1&={frac {5t}{2^{t}}}\[5pt]1&=5te^{-tln 2}\[5pt]{frac {1}{5}}&=te^{-tln 2}\[5pt]-{frac {ln 2}{5}}&=(-tln 2)e^{-tln 2}\[5pt]Wleft(-{frac {ln 2}{5}}right)&=-tln 2\[5pt]t&=-{frac {Wleft(-{frac {ln 2}{5}}right)}{ln 2}}.end{aligned}}}

More generally, the equation

px=ax+b{displaystyle p^{x}=ax+b}

where

p>0 and p≠1 and a≠0{displaystyle p>0{text{ and }}pneq 1{text{ and }}aneq 0}

can be transformed via the substitution of variables

−t=x+ba{displaystyle -t=x+{frac {b}{a}}}

into

tpt=R=−1ap−ba,{displaystyle tp^{t}=R=-{frac {1}{a}}p^{-{frac {b}{a}}},}

giving

t=W(Rln⁡p)ln⁡p,{displaystyle t={frac {W(Rln p)}{ln p}},}

which yields the final solution

x=−W(−ln⁡pap−ba)ln⁡p−ba.{displaystyle x=-{frac {Wleft(-{frac {ln p}{a}},p^{-{frac {b}{a}}}right)}{ln p}}-{frac {b}{a}}.}

Example 2

xx=zxln⁡x=ln⁡zeln⁡x⋅ln⁡x=ln⁡zln⁡x=W(ln⁡z)x=eW(ln⁡z).{displaystyle {begin{aligned}x^{x}&=z\xln x&=ln z\e^{ln x}cdot ln x&=ln z\ln x&=W(ln z)\x&=e^{W(ln z)}.end{aligned}}}

For z ≠ 1, this can be equivalently written as

x=ln⁡zW(ln⁡z),{displaystyle x={frac {ln z}{W(ln z)}},}

since

ln⁡z=W(ln⁡z)eW(ln⁡z){displaystyle ln z=W(ln z)e^{W(ln z)}}

by definition.

Example 3

xn=e−ax, a,n≠0,xneax=1.{displaystyle {begin{aligned}x^{n}&=e^{-ax},quad a,nneq 0,\x^{n}e^{ax}&=1.end{aligned}}}

If n is rational, let ω be any pth root of unity, where p/q =|n| is a reduced fraction. Otherwise, ω=1.

Taking the nth root:

xeaxn=ωaxneaxn=aωnaxn=W(aωn)x=nW(aωn)a.{displaystyle {begin{aligned}xe^{frac {ax}{n}}&=omega \{frac {ax}{n}}e^{frac {ax}{n}}&={frac {aomega }{n}}\{frac {ax}{n}}&=Wleft({frac {aomega }{n}}right)\x&={frac {nWleft({frac {aomega }{n}}right)}{a}}.end{aligned}}}

If we want the real solutions, and a/n is real, we must have ω = ±1 and aω/n > -1/e. This gives at most three solutions:

x={naW0(an),if an≥−1e,naW−1(an),if −1e<an<0.{displaystyle x={begin{cases}{frac {n}{a}}W_{0}left({frac {a}{n}}right),&{text{if }}{frac {a}{n}}geq -{frac {1}{e}},\{frac {n}{a}}W_{-1}left({frac {a}{n}}right),&{text{if }}{-{frac {1}{e}}}<{frac {a}{n}}<0.end{cases}}}

And, if n is rational and p is even:

x={naW0(−an),if an≤1e,naW−1(−an),if 1e>an>0.{displaystyle x={begin{cases}{frac {n}{a}}W_{0}left({frac {-a}{n}}right),&{text{if }}{frac {a}{n}}leq {frac {1}{e}},\{frac {n}{a}}W_{-1}left({frac {-a}{n}}right),&{text{if }}{frac {1}{e}}>{frac {a}{n}}>0.end{cases}}}

Example 4

Whenever the complex infinite exponential tetration

zzz⋅⋅⋅{displaystyle z^{z^{z^{cdot ^{cdot ^{cdot }}}}}}

converges, the Lambert W function provides the actual limit value as

c=exp⁡(−W(−ln⁡z)),{displaystyle c=exp(-W(-ln z)),}

where ln z denotes the principal branch of the complex logarithm. This can be shown by observing that z^c = c if c exists, so

z=c1cz−1=c−1c1z=(1c)1c−ln⁡(z)=1cln⁡1c−ln⁡(z)=eln⁡1cln⁡1cln⁡1c=W(−ln⁡z)1c=eW(−ln⁡z)c=e−W(−ln⁡z),{displaystyle {begin{aligned}z&=c^{frac {1}{c}}\z^{-1}&=c^{-{frac {1}{c}}}\{frac {1}{z}}&=left({frac {1}{c}}right)^{frac {1}{c}}\-ln(z)&={frac {1}{c}}ln {frac {1}{c}}\-ln(z)&=e^{ln {frac {1}{c}}}ln {frac {1}{c}}\ln {frac {1}{c}}&=W(-ln z)\{frac {1}{c}}&=e^{W(-ln z)}\c&=e^{-W(-ln z)},\end{aligned}}}

which is the result which was to be found.

Example 5

Solutions for

xlogb⁡x=a{displaystyle xlog _{b}x=a}

have the form^[5]

x=eW(aln⁡b).{displaystyle x=e^{W(aln b)}.}

Example 6

The solution for the current in a series diode/resistor circuit can also be written in terms of the Lambert W function. See diode modeling.

Example 7

The delay differential equation

y˙(t)=ay(t−1){displaystyle {dot {y}}(t)=ay(t-1)}

has characteristic equation

λ=ae−λ,{displaystyle lambda =ae^{-lambda },}

leading to

λ=Wk(a)andy(t)=eWk(a)t,{displaystyle lambda =W_{k}(a)quad {text{and}}quad y(t)=e^{W_{k}(a)t},}

where k is the branch index. If a ≥ 1/e, only W₀(a) need be considered.

Applications

Instrument design

The Lambert W function was shown in 2013 to be the optimal solution for the required magnetic field of a Zeeman slower.^[15]

Viscous flows

Granular and debris flow fronts and deposits, and the fronts of viscous fluids in natural events and in the laboratory experiments can be described by using the Lambert–Euler omega function as follows:

H(x)=1+W((H(0)−1)e(H(0)−1)−xL),{displaystyle H(x)=1+Wleft((H(0)-1)e^{(H(0)-1)-{frac {x}{L}}}right),}

where H(x) is the debris flow height, x is the channel downstream position, L is the unified model parameter consisting of several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient.

In pipe flow, the Lambert W function is part of the explicit formulation of the Colebrook equation for finding the Darcy friction factor. This factor is used to determine the pressure drop through a straight run of pipe when the flow is turbulent.^[16]

Neuroimaging

The Lambert W function was employed in the field of neuroimaging for linking cerebral blood flow and oxygen consumption changes within a brain voxel, to the corresponding blood oxygenation level dependent (BOLD) signal.^[17]

Chemical engineering

The Lambert W function was employed in the field of chemical engineering for modelling the porous electrode film thickness in a glassy carbon based supercapacitor for electrochemical energy storage. The Lambert W function turned out to be the exact solution for a gas phase thermal activation process where growth of carbon film and combustion of the same film compete with each other.^[18][19]

Materials science

The Lambert W function was employed in the field of epitaxial film growth for the determination of the critical dislocation onset film thickness. This is the calculated thickness of an epitaxial film, where due to thermodynamic principles the film will develop crystallographic dislocations in order to minimise the elastic energy stored in the films. Prior to application of Lambert W for this problem, the critical thickness had to be determined via solving an implicit equation. Lambert W turns it in an explicit equation for analytical handling with ease.^[20]

Porous media

The Lambert W function has been employed in the field of fluid flow in porous media to model the tilt of an interface separating two gravitationally segregated fluids in a homogeneous tilted porous bed of constant dip and thickness where the heavier fluid, injected at the bottom end, displaces the lighter fluid that is produced at the same rate from the top end. The principal branch of the solution corresponds to stable displacements while the −1 branch applies if the displacement is unstable with the heavier fluid running underneath the ligther fluid.^[21]

Bernoulli numbers and Todd genus

The equation (linked with the generating functions of Bernoulli numbers and Todd genus):

Y=X1−eX{displaystyle Y={frac {X}{1-e^{X}}}}

can be solved by means of the two real branches W₀ and W₋₁:

X(Y)={W−1(YeY)−W0(YeY)=Y−W0(YeY)for Y<−1,W0(YeY)−W−1(YeY)=Y−W−1(YeY)for −1<Y<0.{displaystyle X(Y)={begin{cases}W_{-1}left(Ye^{Y}right)-W_{0}left(Ye^{Y}right)=Y-W_{0}left(Ye^{Y}right)&{text{for }}Y<-1,\W_{0}left(Ye^{Y}right)-W_{-1}left(Ye^{Y}right)=Y-W_{-1}left(Ye^{Y}right)&{text{for }}-1<Y<0.end{cases}}}

This application shows that the branch difference of the W function can be employed in order to solve other transcendental equations.^[22]

Statistics

The centroid of a set of histograms defined with respect to the symmetrized Kullback–Leibler divergence (also called the Jeffreys divergence) has a closed form using the Lambert W function.^[23]

Exact solutions of the Schrödinger equation

The Lambert W function appears in a quantum-mechanical potential (see Lambert W step potential) which affords the fifth – next to those of the harmonic oscillator plus centrifugal, the Coulomb plus inverse square, the Morse, and the inverse square root potential – exact solution to the stationary one-dimensional Schrödinger equation in terms of the confluent hypergeometric functions. The potential is given as

V=V01+W(e−xσ).{displaystyle V={frac {V_{0}}{1+Wleft(e^{-{frac {x}{sigma }}}right)}}.}

A peculiarity of the solution is that each of the two fundamental solutions that compose the general solution of the Schrödinger equation is given by a combination of two confluent hypergeometric functions of an argument proportional to^[24]

z=W(e−xσ).{displaystyle z=Wleft(e^{-{frac {x}{sigma }}}right).}

Exact solutions of the Einstein vacuum equations

In the Schwarzschild metric solution of the Einstein vacuum equations, the W function is needed to go from the Eddington-Finkelstein coordinates to the Schwarzschild coordinates. For this reason, it also appears in the construction of the Kruskal–Szekeres coordinates.

Resonances of the delta-shell potential

The s-wave resonances of the delta-shell potential can be written exactly in terms of the Lambert W function.^[25]

Thermodynamic equilibrium

If a reaction involves reactants and products having heat capacities that are constant with temperature then the equilibrium constant K obeys

ln⁡K=aT+b+cln⁡T{displaystyle ln K={frac {a}{T}}+b+cln T}

for some constants a, b, and c. When c (equal to ΔC_p / R) is not zero we can find the value or values of T where K equals a given value as follows, where we use L for ln T.

−a=(b−ln⁡K)T+cTln⁡T=(b−ln⁡K)eL+cLeL−ac=(b−ln⁡Kc+L)eL−aceb−ln⁡Kc=(L+b−ln⁡Kc)eL+b−ln⁡KcL=W(−aceb−ln⁡Kc)+ln⁡K−bcT=exp⁡(W(−aceb−ln⁡Kc)+ln⁡K−bc).{displaystyle {begin{aligned}-a&=(b-ln K)T+cTln T\&=(b-ln K)e^{L}+cLe^{L}\[5pt]-{frac {a}{c}}&=left({frac {b-ln K}{c}}+Lright)e^{L}\[5pt]-{frac {a}{c}}e^{frac {b-ln K}{c}}&=left(L+{frac {b-ln K}{c}}right)e^{L+{frac {b-ln K}{c}}}\[5pt]L&=Wleft(-{frac {a}{c}}e^{frac {b-ln K}{c}}right)+{frac {ln K-b}{c}}\[5pt]T&=exp left(Wleft(-{frac {a}{c}}e^{frac {b-ln K}{c}}right)+{frac {ln K-b}{c}}right).end{aligned}}}

If a and c have the same sign there will be either two solutions or none (or one if the argument of W is exactly −1/e). (The upper solution may not be relevant.) If they have opposite signs, there will be one solution.

AdS/CFT correspondence

The classical finite-size corrections to the dispersion relations of giant magnons, single spikes and GKP strings can be expressed in terms of the Lambert W function.^[26][27]

Generalizations

The standard Lambert W function expresses exact solutions to transcendental algebraic equations (in x) of the form:

e−cx=a0(x−r){displaystyle e^{-cx}=a_{0}(x-r)}

(1)

where a₀, c and r are real constants. The solution is

x=r+1cW(ce−cra0).{displaystyle x=r+{frac {1}{c}}Wleft({frac {c,e^{-cr}}{a_{0}}}right).}

Generalizations of the Lambert W function^[28][29][30] include:

• An application to general relativity and quantum mechanics (quantum gravity) in lower dimensions, in fact a previously unknown link (unknown prior to 2007^[31]) between these two areas, where the right-hand side of (1) is now a quadratic polynomial in x:

e−cx=a0(x−r1)(x−r2),{displaystyle e^{-cx}=a_{0}left(x-r_{1}right)left(x-r_{2}right),}

(2)

where r₁ and r₂ are real distinct constants, the roots of the quadratic polynomial. Here, the solution is a function has a single argument x but the terms like r_i and a₀ are parameters of that function. In this respect, the generalization resembles the hypergeometric function and the Meijer G function but it belongs to a different class of functions. When r₁ = r₂, both sides of (2) can be factored and reduced to (1) and thus the solution reduces to that of the standard W function. Equation (2) expresses the equation governing the dilaton field, from which is derived the metric of the R = T or lineal two-body gravity problem in 1 + 1 dimensions (one spatial dimension and one time dimension) for the case of unequal rest masses, as well as the eigenenergies of the quantum-mechanical double-well Dirac delta function model for unequal charges in one dimension.

• Analytical solutions of the eigenenergies of a special case of the quantum mechanical three-body problem, namely the (three-dimensional) hydrogen molecule-ion.^[32] Here the right-hand side of (1) (or (2)) is now a ratio of infinite order polynomials in x:

e−cx=a0∏i=1∞(x−ri)∏i=1∞(x−si){displaystyle e^{-cx}=a_{0}{frac {displaystyle prod _{i=1}^{infty }(x-r_{i})}{displaystyle prod _{i=1}^{infty }(x-s_{i})}}}

(3)

where r_i and s_i are distinct real constants and x is a function of the eigenenergy and the internuclear distance R. Equation (3) with its specialized cases expressed in (1) and (2) is related to a large class of delay differential equations. G. H. Hardy's notion of a "false derivative" provides exact multiple roots to special cases of (3).^[33]

Applications of the Lambert W function in fundamental physical problems are not exhausted even for the standard case expressed in (1) as seen recently in the area of atomic, molecular, and optical physics.^[34]

Plots

• Plots of the Lambert W function on the complex plane


• 
  

  

  
  

  
  

  z = Re(W₀(x + iy))
  

  
  

  
  


• 
  

  

  
  

  
  

  z = Im(W₀(x + iy))
  

  
  

  
  


• 
  

  

  
  

  
  

  z = |W₀(x + iy)|
  

  
  

  
  


• 
  

  

  
  

  
  

  Superimposition of the previous three plots
  

  
  

  
  

Numerical evaluation

The W function may be approximated using Newton's method, with successive approximations to w = W(z) (so z = we^w) being

wj+1=wj−wjewj−zewj+wjewj.{displaystyle w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}+w_{j}e^{w_{j}}}}.}

The W function may also be approximated using Halley's method,

wj+1=wj−wjewj−zewj(wj+1)−(wj+2)(wjewj−z)2wj+2{displaystyle w_{j+1}=w_{j}-{frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}left(w_{j}+1right)-{dfrac {left(w_{j}+2right)left(w_{j}e^{w_{j}}-zright)}{2w_{j}+2}}}}}

given in Corless et al.^[2] to compute W.

Software

The Lambert W function is implemented as
LambertW in Maple, lambertw in GP (and glambertW in PARI), lambertw in Matlab,^[35] also lambertw in octave with the specfun package, as lambert_w in Maxima,^[36] as ProductLog (with a silent alias LambertW) in Mathematica,^[37] as lambertw in Python scipy's special function package,^[38] as LambertW in Perl's ntheory module,^[39] and as gsl_sf_lambert_W0, gsl_sf_lambert_Wm1 functions in the special functions section of the GNU Scientific Library (GSL). In the Boost C++ libraries, the calls are lambert_w0, lambert_wm1, lambert_w0_prime, and lambert_wm1_prime. In R, the Lambert W function is implemented as the lambertW0 and lambertWm1 functions in the lamW package.^[40]

A C++ code for all the branches of the complex Lambert W function is available on the homepage of István Mező.^[41]

See also

• Wright Omega function


• Lambert's trinomial equation
  


• Lagrange inversion theorem


• Experimental mathematics


• Holstein–Herring method


• 
  R = T model


• Ross' π lemma

Notes

1. 
   ^ Chow, Timothy Y. (1999), "What is a closed-form number?", American Mathematical Monthly, 106 (5): 440–448, arXiv:math/9805045, doi:10.2307/2589148, JSTOR 2589148, MR 1699262.mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}.
   


2. 
   ^ ^abcde Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). "On the Lambert W function" (PostScript). Advances in Computational Mathematics. 5: 329–359. doi:10.1007/BF02124750.
   


3. 
   ^ Lambert J. H., "Observationes variae in mathesin puram", Acta Helveticae physico-mathematico-anatomico-botanico-medica, Band III, 128–168, 1758.
   


4. 
   ^ Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus". Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921.
   


5. 
   ^ ^ab Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J. (1993). "Lambert's W function in Maple". The Maple Technical Newsletter. 9: 12–22. CiteSeerX 10.1.1.33.2556.
   


6. 
   ^ A. Hoorfar, M. Hassani, Inequalities on the Lambert W Function and Hyperpower Function, JIPAM, volume 9, issue 2, article 51. 2008.
   


7. 
   ^ Chatzigeorgiou, I. (2013). "Bounds on the Lambert function and their Application to the Outage Analysis of User Cooperation". IEEE Communications Letters. 17 (8): 1505–1508. arXiv:1601.04895. doi:10.1109/LCOMM.2013.070113.130972.
   


8. 
   ^ "Lambert function: Identities (formula 01.31.17.0001)".
   


9. 
   ^ "Lambert W-Function".
   


10. 
    ^ Finch, S. R. (2003). Mathematical constants. Cambridge University Press. p. 450.
    


11. 
    ^ István, Mező. "An integral representation for the principal branch of Lambert the W function". Retrieved 7 November 2017.
    


12. 
    ^ Dubinov, A. E.; Dubinova, I. D.; Saǐkov, S. K. (2006). The Lambert W Function and Its Applications to Mathematical Problems of Physics (in Russian). RFNC-VNIIEF. p. 53.
    


13. 
    ^ Robert M., Corless; David J., Jeffrey; Donald E., Knuth (1997). A sequence of series for the Lambert W function. Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation. pp. 197–204. doi:10.1145/258726.258783. ISBN 978-0897918756.
    


14. 
    ^ "The Lambert W Function". Ontario Research Centre.
    


15. 
    ^ B Ohayon., G Ron. (2013). "New approaches in designing a Zeeman Slower". Journal of Instrumentation. 8 (2): P02016. arXiv:1212.2109. Bibcode:2013JInst...8P2016O. doi:10.1088/1748-0221/8/02/P02016.
    


16. 
    ^ More, A. A. (2006). "Analytical solutions for the Colebrook and White equation and for pressure drop in ideal gas flow in pipes". Chemical Engineering Science. 61 (16): 5515–5519. doi:10.1016/j.ces.2006.04.003.
    


17. 
    ^ Sotero, Roberto C.; Iturria-Medina, Yasser (2011). "From Blood oxygenation level dependent (BOLD) signals to brain temperature maps". Bull Math Biol (Submitted manuscript). 73 (11): 2731–47. doi:10.1007/s11538-011-9645-5. PMID 21409512.
    


18. 
    ^ Braun, Artur; Wokaun, Alexander; Hermanns, Heinz-Guenter (2003). "Analytical Solution to a Growth Problem with Two Moving Boundaries". Appl Math Model. 27 (1): 47–52. doi:10.1016/S0307-904X(02)00085-9.
    


19. 
    ^ Braun, Artur; Baertsch, Martin; Schnyder, Bernhard; Koetz, Ruediger (2000). "A Model for the film growth in samples with two moving boundaries – An Application and Extension of the Unreacted-Core Model". Chem Eng Sci. 55 (22): 5273–5282. doi:10.1016/S0009-2509(00)00143-3.
    


20. 
    ^ Braun, Artur; Briggs, Keith M.; Boeni, Peter (2003). "Analytical solution to Matthews' and Blakeslee's critical dislocation formation thickness of epitaxially grown thin films". J Cryst Growth. 241 (1–2): 231–234. Bibcode:2002JCrGr.241..231B. doi:10.1016/S0022-0248(02)00941-7.
    


21. 
    ^ Colla, Pietro (2014). "A New Analytical Method for the Motion of a Two-Phase Interface in a Tilted Porous Medium". PROCEEDINGS,Thirty-Eighth Workshop on Geothermal Reservoir Engineering,Stanford University. SGP-TR-202.([1])
    


22. 
    ^ D. J. Jeffrey and J. E. Jankowski, "Branch differences and Lambert W"
    


23. 
    ^ F. Nielsen, "Jeffreys Centroids: A Closed-Form Expression for Positive Histograms and a Guaranteed Tight Approximation for Frequency Histograms"
    


24. 
    ^ A.M. Ishkhanyan, "The Lambert W barrier – an exactly solvable confluent hypergeometric potential".
    


25. 
    ^ de la Madrid, R. (2017). "Numerical calculation of the decay widths, the decay constants, and the decay energy spectra of the resonances of the delta-shell potential". Nucl. Phys. A. 962: 24–45. arXiv:1704.00047. Bibcode:2017NuPhA.962...24D. doi:10.1016/j.nuclphysa.2017.03.006.
    


26. 
    ^ Floratos, Emmanuel; Georgiou, George; Linardopoulos, Georgios (2014). "Large-Spin Expansions of GKP Strings". JHEP. 03 (3): 0180. arXiv:1311.5800. doi:10.1007/JHEP03(2014)018.
    


27. 
    ^ Floratos, Emmanuel; Linardopoulos, Georgios (2015). "Large-Spin and Large-Winding Expansions of Giant Magnons and Single Spikes". Nucl. Phys. B. 897: 229–275. arXiv:1406.0796. doi:10.1016/j.nuclphysb.2015.05.021.
    


28. 
    ^ Scott, T. C.; Mann, R. B.; Martinez Ii, Roberto E. (2006). "General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function". AAECC (Applicable Algebra in Engineering, Communication and Computing). 17 (1): 41–47. arXiv:math-ph/0607011. doi:10.1007/s00200-006-0196-1.
    


29. 
    ^ Scott, T. C.; Fee, G.; Grotendorst, J. (2013). "Asymptotic series of Generalized Lambert W Function". SIGSAM (ACM Special Interest Group in Symbolic and Algebraic Manipulation). 47 (185): 75–83. doi:10.1145/2576802.2576804.
    


30. 
    ^ Scott, T. C.; Fee, G.; Grotendorst, J.; Zhang, W.Z. (2014). "Numerics of the Generalized Lambert W Function". SIGSAM. 48 (1/2): 42–56. doi:10.1145/2644288.2644298.
    


31. 
    ^ Farrugia, P. S.; Mann, R. B.; Scott, T. C. (2007). "N-body Gravity and the Schrödinger Equation". Class. Quantum Grav. 24 (18): 4647–4659. arXiv:gr-qc/0611144. Bibcode:2007CQGra..24.4647F. doi:10.1088/0264-9381/24/18/006.
    


32. 
    ^ Scott, T. C.; Aubert-Frécon, M.; Grotendorst, J. (2006). "New Approach for the Electronic Energies of the Hydrogen Molecular Ion". Chem. Phys. 324 (2–3): 323–338. arXiv:physics/0607081. Bibcode:2006CP....324..323S. CiteSeerX 10.1.1.261.9067. doi:10.1016/j.chemphys.2005.10.031.
    


33. 
    ^ Maignan, Aude; Scott, T. C. (2016). "Fleshing out the Generalized Lambert W Function". SIGSAM. 50 (2): 45–60. doi:10.1145/2992274.2992275.
    


34. 
    ^ Scott, T. C.; Lüchow, A.; Bressanini, D.; Morgan, J. D. III (2007). "The Nodal Surfaces of Helium Atom Eigenfunctions". Phys. Rev. A. 75 (6): 060101. Bibcode:2007PhRvA..75f0101S. doi:10.1103/PhysRevA.75.060101.
    


35. 
    ^ lambertw – MATLAB
    


36. 
    ^ Maxima, a Computer Algebra System
    


37. 
    ^ ProductLog at WolframAlpha
    


38. 
    ^ "Scipy.special.lambertw — SciPy v0.16.1 Reference Guide".
    


39. 
    ^ ntheory at MetaCPAN
    


40. 
    ^ Adler, Avraham (2017-04-24), lamW: Lambert W Function, retrieved 2017-12-19
    


41. 
    ^ The webpage of István Mező
    

References

• 
  Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996). "On the Lambert W function" (PDF). Advances in Computational Mathematics. 5: 329–359. doi:10.1007/BF02124750. ISSN 1019-7168
  


• 
  Chapeau-Blondeau, F.; Monir, A. (2002). "Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2" (PDF). IEEE Trans. Signal Process. 50 (9).
  


• 
  Francis; et al. (2000). "Quantitative General Theory for Periodic Breathing". Circulation. 102 (18): 2214–21. CiteSeerX 10.1.1.505.7194. doi:10.1161/01.cir.102.18.2214. PMID 11056095. (Lambert function is used to solve delay-differential dynamics in human disease.)


• 
  Hayes, B. (2005). "Why W?" (PDF). American Scientist. 93 (2): 104–108. doi:10.1511/2005.2.104.
  


• 
  Roy, R.; Olver, F. W. J. (2010), "Lambert W function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
  


• 
  Stewart, Seán M. (2005). "A New Elementary Function for Our Curricula?" (PDF). Australian Senior Mathematics Journal. 19 (2): 8–26. ISSN 0819-4564. ERIC EJ720055. Lay summary.
  


• 
  Veberic, D., "Having Fun with Lambert W(x) Function" arXiv:1003.1628 (2010); Veberic, D. (2012). "Lambert W function for applications in physics". Computer Physics Communications. 183 (12): 2622–2628. arXiv:1209.0735. Bibcode:2012CoPhC.183.2622V. doi:10.1016/j.cpc.2012.07.008.
  


• 
  Chatzigeorgiou, I. (2013). "Bounds on the Lambert function and their Application to the Outage Analysis of User Cooperation". IEEE Communications Letters. 17 (8): 1505–1508. arXiv:1601.04895. doi:10.1109/LCOMM.2013.070113.130972.
  

External links

Wikimedia Commons has media related to Lambert W function.

• National Institute of Science and Technology Digital Library – Lambert W


• MathWorld – Lambert W-Function


• Computing the Lambert W function


• Corless et al. Notes about Lambert W research


• GPL C++ implementation with Halley's and Fritsch's iteration.


• 
  Special Functions of the GNU Scientific Library – GSL

This page is only for reference, If you need detailed information, please check here