十二面體
部分的十二面體 | |
|---|---|
 五角十二面體 |  扭稜楔形體 |
 正十二面體 |  菱形十二面體 |
 十角柱 |  雙四角錐柱 |
在幾何學中,十二面體是指由十二個面組成的多面體,而由十二個全等的正五邊形組成的十二面體稱為正十二面體。
十二個面的多面體可以是正十二面體、菱形十二面體、正五角帳塔、雙四角錐柱、變稜雙五角椎、十一角錐、十角柱。
目录
1 常見的十二面體
1.1 十角柱
1.2 十一角錐
1.3 詹森多面體
1.4 十二面體列表
2 參見
3 參考文獻
常見的十二面體
在所有凸十二面體中,包含鏡射像共有6,384,634種拓樸結構明顯差異的凸十二面體[1][2]。拓樸結構有明顯差異意味著兩種多面體無法透過移動頂點位置、扭曲或伸縮來相互變換的多面體,例如正十二面體和十角柱無論如何變形都無法互相變換,因此拓樸結構不同,但正十二面體和截角五方偏方面體可以透過簡單的變形來彼此互換,因此正十二面體和截角五方偏方面體在拓樸上並無明顯差異。
十角柱
十角柱是一種底面為十邊形的柱體,由12個面30條邊和20個頂點組成。正十角柱代表每個面都是正多邊形的十角柱,其每個頂點都是2個正方形和1個十邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正十二面體。
十一角錐
十一角錐是一種底面為十一邊形的錐體,其具有12個面、22條邊和12個頂點,其對偶多面體是自己本身。正十一角錐是一種底面為正十一邊形的十一角錐。
詹森多面體
在十一面體中,有4個是詹森多面體,它們分別為:正五角帳塔、變稜雙五角椎、雙四角錐柱、正二十面體欠二側錐。
| 名稱 | 種類 | 圖像 | 編號 | 頂點 | 邊 | 面 | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|
| 正五角帳塔 | 帳塔 |  | J5 | 15 | 25 | 12 | 5個正三角形 5個正方形 1個正五邊形 1個正十邊形 | C5v, [5], (*55) |  |
| 變稜雙五角椎 | 變稜錐 |  | J84 | 8 | 18 | 12 | 12個正三角形 | D2d |  |
| 雙四角錐柱 | 雙錐柱 | 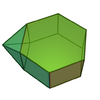 | J15 | 10 | 20 | 12 | 8個正三角形 4個正方形 | D4h, [4,2], (*422) |  |
| 正二十面體欠二側錐 | 切割二十面體 |  | J62 | 10 | 20 | 12 | 10個正三角形 2個五邊形 | C2v |  |
十二面體列表
| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
正十二面體 | 正多面體 |  | {5,3} | 20 | 30[3] | 12 | 2 | 12個正五邊形 | Ih, H3, [5,3], (*532) |  |
| 十角柱 | 稜柱體 |  | t{2,10} {10}x{} | 20 | 30[4] | 12 | 2 | 2個十邊形 10個矩形 | D10h, [8,2], (*10 2 2), order 40 | |
| 十一角錐 | 稜錐體 | ( ) ∨ {11} | 12 | 22 | 12 | 2 | 1個十一邊形 11個三角形 | C11v, [11], (*11 11)[5] | ||
| 雙六角錐 | 雙錐體 | 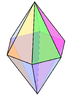 | { } + {6} | 8 | 18 | 12 | 2 | 12個三角形 | D6h, [6,2], (*226), order 24 | |
五角反柱 | 反稜柱 |  | s{2,5} | 10 | 20 | 12 | 2 | 2個五邊形 10個三角形 | D5d, [2+,10], (2*5), order 20 |  |
| Ih, 120階 | |||
|---|---|---|---|
正- | 小星形- | 大- | 大星形- |
 |  |  |  |
| Th, 24階 | T, 12階 | Oh, 48階 | Td, 24階 |
五角十二面體 | 五角三四面體 | 菱形- | 鳶形- |
 |  |  |  |
| D4h, 16階 | D3h, 12階 | ||
菱形六角化- | 菱形四角化- | 梯形菱形- | 梯形鳶形- |
 |  |  |  |
參見
正十二面體烷(化學)
參考文獻
^ Steven Dutch: How Many Polyhedra are There? 页面存档备份,存于互联网档案馆
^ Counting polyhedra numericana.com [2016-1-10]
^ Sutton, Daud, Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA: 55, 2002, ISBN 9780802713865
^ The Decagonal Prism. eusebeia. [2016-08-21].
^ Simplest Canonical Polyhedron with C11v Symmetry. dmccooey. [2016-08-21].
| ||||||||||||||||||
|

Comments
Post a Comment