概念文字

最初1879年版的标题页。

《概念文字》是1879年出版的戈特洛布·弗雷格写的一本关于逻辑学的书。书名《Begriffsschrift》通常翻译成《Concept Writing》或《Concept Notation》；书的完整标题把它标识为《模仿算术的纯思维的形式语言》。这本小书无可争议是亚里士多德之后在逻辑学领域最重要的出版物。弗雷格开发他的形式逻辑系统的动机是类似于莱布尼兹对“演算推论器”的渴望。

弗雷格定义了逻辑演算来支持他在数学基础上的研究。“概念文字”是书和其中定义的演算二者的名字。

目录

• 
  1 记号和系统
  


• 
  2 弗雷格著作中的演算
  


• 
  3 对其他著作的影响
  


• 
  4 一段引文
  


• 
  5 引用
  


• 
  6 参见
  


• 
  7 外部链接
  

记号和系统

演算介入了量词，因而本质上是经典的谓词逻辑，尽管使用了一种特异的二维记号（notation）：连结词和量词使用连接公式的线条来书写，而不是今天使用的符号（symbol）¬、∧、∀。例如，在判断B和A之间的蕴涵，也就是B→A{displaystyle Brightarrow A}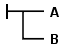用来指定。

在他的著作的第一章中，弗雷格确定了基本概念和标号（sign），象命题（"断定／判断"），和全称量词（"普遍性"），蘊涵（"条件性"），否定和等号≡{displaystyle equiv }；在第二章中他声明了九个形式化的命题作为公理（它们是在语义上证明了的形式化陈述）。

基本概念	Frege記號	現代記號
斷定	⊢A,⊩A{displaystyle vdash A,Vdash A,}	p(A)=1{displaystyle p(A)=1,} p(A)=i{displaystyle p(A)=i,}
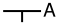
否定		¬A,∼A{displaystyle neg A,sim A,}
條件（蘊涵）		B⇒A{displaystyle BRightarrow A} B⊂A{displaystyle Bsubset A,}
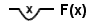
全称量化		∀x:Φ(x){displaystyle forall xcolon Phi (x)}
存在量化		∃x:Φ(x){displaystyle exists xcolon Phi (x)}
內容同一（等號）	A≡B{displaystyle Aequiv B,}	A=B{displaystyle A=B,}

他给出了条件的定义（第1章。§5.）:

"设A和B指称可断定的内容，则有四种潜在的可能性：

(1)	A被肯定了（assert）, B被肯定了；
(2)	A被肯定了，B被否定了；
(3)	A被否定了，B被肯定了；
(4)	A被否定了，B被否定了。

设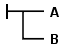标示（sign）第三种可能性是不能得到的，而只能是其他三种中的一个。所以如果我们否定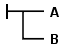就意味着第三种可能性是有效的，就是说我们否定了A并肯定了B。"

弗雷格著作中的演算

弗雷格声明了九个重言式断定作为公理。他以语义方式证明了它们，并以语法上的演绎证明了其他重言式断定。

1. ⊢  A→(B→A){displaystyle vdash Arightarrow left(Brightarrow Aright)}


2. ⊢  [ A→(B→C) ] → [ (A→B)→(A→C) ]{displaystyle vdash left[ Arightarrow left(Brightarrow Cright) right] rightarrow left[ left(Arightarrow Bright)rightarrow left(Arightarrow Cright) right]}


3. ⊢  [ D→(B→A) ] → [ B→(D→A) ]{displaystyle vdash left[ Drightarrow left(Brightarrow Aright) right] rightarrow left[ Brightarrow left(Drightarrow Aright) right]}


4. ⊢  (B→A) → (¬A→¬B){displaystyle vdash left(Brightarrow Aright) rightarrow left(lnot Arightarrow lnot Bright)}


5. ⊢  ¬¬A→A{displaystyle vdash lnot lnot Arightarrow A}


6. ⊢  A→¬¬A{displaystyle vdash Arightarrow lnot lnot A}


7. ⊢  (c=d)→(f(c)=f(d)){displaystyle vdash left(c=dright)rightarrow left(f(c)=f(d)right)}


8. ⊢  c=c{displaystyle vdash c=c}


9. ⊢  ( ∀a:f(a) ) → f(c){displaystyle vdash left( forall a:f(a) right) rightarrow f(c)}

弗雷格在第二章中历数了被形式化的命题；成为了他的公理的是第1^st, 2^nd, 8^th, 28^th, 31^st, 41^st, 52^nd, 54^th, 58^th个命题。

他在这章中还声明了两个推理规则：它们是肯定前件；和代换律。在第一章中他宣布了一个约定，即“普遍化律”。这意味着如果“自由变量”能在一个断定中找到，则把它当作全称量化的，依据弗雷格的定律，在⊢{displaystyle vdash }标号（“断定符号”）之后的，被固定的（fixed）变量是断定，而不是“开放”的公式，也就是谓词。

弗雷格在第二和第三章中在语法上证明了一百多个形式陈述。第三章（"Parts from a general series theory"）是对他在建造算术上做的工作的介绍。

对其他著作的影响

它的记号的某些痕跡幸存了：被逻辑学家非正式的叫做“十字转门”（turnstile）的符号⊢{displaystyle vdash }演化自弗雷格的“Inhaltsstrich”─和“Urteilsstrich”│。弗雷格在《Begriffsschrift》中以合一的形式├─使用这些符号来声明一个命题是（重言式）真的，而不是简单的宣布它。他使用“Definitionsdoppelstrich”│├─作为表示一个命题是一个定义的符号。

在逻辑哲学论中，维特根斯坦通过使用术语“Begriffsschrift”作为逻辑形式主义的同义词来表达对弗雷格的敬意。

在弗雷格后来的著作《意义和引用》中，它放弃了在本书中关于同一性达成的某些结论（用数学上的 = 号来标记）。

一段引文

"如果哲学的任务是打破言辞在表达人类思想上的统治[...]，那么我的概念记号，就是为这个目的而开发的，它能够成为哲学家的有用的工具[...]我认为，只是通过发明这些概念记号，逻辑的本质（matter）就已经被促进了（forward）。"

Begriffsschrift [前言]

引用

• 
  Gottlob Frege。Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle, 1879.


• Risto Vilkko, 1998. 'The reception of Frege's Begriffsschrift'. Historia Mathematica 25(4):412-422.

参见

• 弗雷格命题演算

外部链接

• "Frege的逻辑学"于Stanford哲学百科全书
  

规范控制 BNF: cb13775933w (data) GND: 4283480-6

This page is only for reference, If you need detailed information, please check here