定態

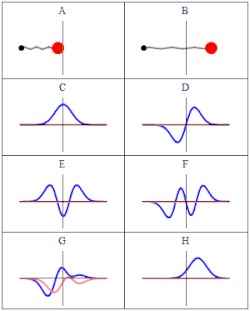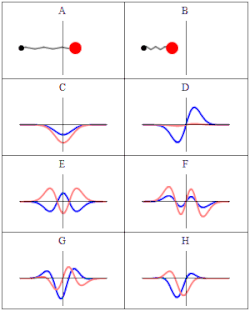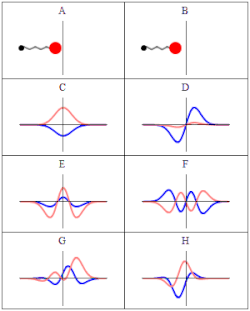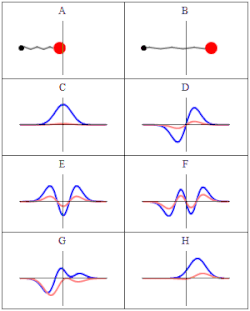
設想經典力學裏的諧振子 系統（A-B），一條彈簧的一端固定不動，另一端有一個帶質量圓球；在量子力學裏， （C-H）展示出同樣系統的薛丁格方程式的六個波函數解。橫軸坐標表示位置，豎軸坐標表示機率幅的實部（藍色）或虛部（紅色）。（C-F）是定態，（G、H）不是定態。定態的能量為駐波振動頻率與約化普朗克常數的乘積。

描述諧振子的含時薛丁格方程式的三個波函數解。左邊：波函數機率幅的實部（藍色）或虛部（紅色）。右邊：找到粒子在某位置的機率，這說明了為甚麼機率與時間無關的量子態被稱為「定態」。上面兩個橫排是定態，最下面橫排是疊加態 ψN=(ψ0+ψ1)/2{displaystyle psi _{N}=(psi _{0}+psi _{1})/{sqrt {2}}} 。

在量子力學裏，定態（stationary state）是一種量子態，定態的機率密度與時間無關。以方程式表式，定態的機率密度對於時間的導數為

ddt|Ψ(x,t)|2=0{displaystyle {frac {d}{dt}}|Psi (x,,t)|^{2}=0} ；

其中，Ψ(x,t){displaystyle Psi (x,,t)} 是定態的波函數，x{displaystyle x} 是位置，t{displaystyle t} 是時間 。

設定一個量子系統的含時薛丁格方程式為

−ℏ22m∂2∂x2Ψ+VΨ=iℏ∂∂tΨ{displaystyle -{frac {hbar ^{2}}{2m}}{frac {partial ^{2}}{partial x^{2}}}Psi +VPsi =ihbar {frac {partial }{partial t}}Psi } ；

其中，ℏ{displaystyle hbar } 是約化普朗克常數，m{displaystyle m} 是質量，V(x){displaystyle V(x)} 是位勢。

這個方程式有一個定態的波函數解：

Ψ(x,t)=ψ(x)e−iEt/ℏ{displaystyle Psi (x,,t)=psi (x)e^{-iEt/hbar }} ；

其中，ψ(x){displaystyle psi (x)} 是 Ψ(x,t){displaystyle Psi (x,,t)} 的不含時間部分，E{displaystyle E} 是能量。

將這定態波函數代入含時薛丁格方程式，則可除去時間關係：

−ℏ22m∂2∂x2ψ+Vψ=Eψ{displaystyle -{frac {hbar ^{2}}{2m}}{frac {partial ^{2}}{partial x^{2}}}psi +Vpsi =Epsi } 。

這是一個不含時薛丁格方程式，可以用來求得本徵能量 E{displaystyle E} 與伴隨的本徵函數 ψE(x){displaystyle psi _{E}(x)} 。定態的能量都是明確的，是定態薛丁格方程式的本徵能量 E{displaystyle E} ，波函數 ψ(x){displaystyle psi (x)} 是定態薛丁格方程式的本徵函數 ψE(x){displaystyle psi _{E}(x)} 。

機率密度與時間無關

雖然定態 Ψ(x,t){displaystyle Psi (x,,t)} 很明顯的含時間。含時間部分是個相位因子。定態的機率密度不含有相位因子這項目：

|Ψ(x,t)|2=|ψ(x)|2{displaystyle |Psi (x,,t)|^{2}=|psi (x)|^{2}} 。

所以，定態的機率密度與時間無關。一個直接的後果就是期望值也都與時間無關。例如，位置的期望值 ⟨x⟩{displaystyle langle xrangle } 是

⟨x⟩=∫−∞∞Ψ∗(x,t)xΨ(x,t)dx=∫−∞∞x|Ψ(x,t)|2dx=∫−∞∞x|ψ(x)|2dx{displaystyle {begin{aligned}langle xrangle &=int _{-infty }^{infty }Psi ^{*}(x,,t)xPsi (x,,t),dx\&=int _{-infty }^{infty },x|Psi (x,,t)|^{2},dx\&=int _{-infty }^{infty },x|psi (x)|^{2},dx\end{aligned}}} 。

再舉一例，動量的期望值 ⟨p⟩{displaystyle langle prangle } 是

⟨p⟩=∫−∞∞Ψ∗(x,t)ℏi∂∂xΨ(x,t)dx=ℏi∫−∞∞ψ(x)eiEt/ℏ∂∂x(ψ(x)e−iEt/ℏ)dx=ℏi∫−∞∞ψ∗(x)∂∂xψ(x)dx{displaystyle {begin{aligned}langle prangle &=int _{-infty }^{infty }Psi ^{*}(x,,t){frac {hbar }{i}}{frac {partial }{partial x}}Psi (x,,t),dx\&={frac {hbar }{i}}int _{-infty }^{infty }psi (x)e^{iEt/hbar }{frac {partial }{partial x}}(psi (x)e^{-iEt/hbar }),dx\&={frac {hbar }{i}}int _{-infty }^{infty },psi ^{*}(x){frac {partial }{partial x}}psi (x),dx\end{aligned}}} 。

所以，⟨x⟩{displaystyle langle xrangle } 和 ⟨p⟩{displaystyle langle prangle } 都與時間無關。一般而言，給予任意一個位置與動量的函數 f(x,p){displaystyle f(x,,p)} ，期望值 ⟨f(x,p)⟩{displaystyle langle f(x,,p)rangle } 必然與時間無關。

參閱

• 純態


• 混合態


• 基態


• 激發態


• 束縛態


• 真空態


• 相干態


• 簡併態

參考文獻

• 
  Griffiths, David J. Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. 2004. ISBN 0-13-111892-7. 
  

This page is only for reference, If you need detailed information, please check here