電磁力

感受到電磁力的作用，移動於磁場中的電子射束，其移動路徑呈圓形。電子經過的路徑會有紫色光發射出來。這是因為電子與玻璃球內的氣體分子碰撞而產生的現象。

電磁力（英语：electromagnetic force）是處於電場、磁場或電磁場的帶電粒子所受到的作用力。大自然的四種基本力中，電磁力是其中一種，其它三種是強作用力、弱作用力、引力。光子是傳遞電磁力的媒介。^[1]:13在電動力學裏，電磁力稱為勞侖茲力。延伸至相對論性量子場論，在量子電動力學裏，兩個帶電粒子倚賴光子為媒介傳遞電磁力。帶電粒子是帶有淨電荷的粒子。電荷是基本粒子的內秉性質。只有帶電粒子或帶電物質（帶有淨電荷的物質）才能夠感受到電磁力，也只有帶電粒子或帶電物質才能夠製成電場、磁場或電磁場來影響其它帶電粒子或帶電物質。

對於決定日常生活所遇到的物質的內部性質，電磁力扮演重要角色。在物質內部，分子與分子之間彼此相互作用的分子間作用力，就是電磁力的一種形式。分子間作用力促使一般物質呈現出各種各樣的物理與化學性質。由於電子與原子核分別帶有的負電荷與正電荷，它們彼此之間會以電磁力相互吸引，使得電子移動於環繞著原子核的原子軌道，與原子核共同組成原子。分子的建構組元是原子。幾個鄰近原子的電子與電子、電子與原子核、原子核與原子核，以電磁力彼此之間相互作用，主導與驅動各種化學反應，因此促成了所有生物程序。^{[2]:6-7[3]:8-9}

目录

• 
  1 概述
  


• 
  2 基本交互作用
  


• 
  3 相對論下的電磁力
  


• 
  4 量子電動力學
  


• 
  5 计量和单位
  


• 
  6 參見
  


• 
  7 參考資料
  

概述

在電動力學裏，若考慮一帶電粒子在電磁場中的受力，可以用以下的勞侖茲力定律表示：

F=q(E+v×B){displaystyle mathbf {F} =q(mathbf {E} +mathbf {v} times mathbf {B} )}；

其中，F{displaystyle mathbf {F} }是勞侖茲力，q{displaystyle q}是帶電粒子的電荷量，E{displaystyle mathbf {E} }是電場，v{displaystyle mathbf {v} }是帶電粒子的速度，B{displaystyle mathbf {B} }是磁場。

勞侖茲力定律是一個基本公理，不是從別的理論推導出來的定律。

這方程式右邊有兩項，第一項是電場力FE=qE{displaystyle mathbf {F} _{E}=qmathbf {E} }，第二項是磁場力FB=qv×B{displaystyle mathbf {F} _{B}=qmathbf {v} times mathbf {B} }。

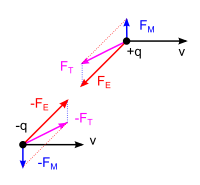
當兩個帶電粒子都以相同速度v{displaystyle mathbf {v} }移動時，帶正電粒子+q{displaystyle +q}會感受到電場力FE{displaystyle mathbf {F} _{E}}、磁場力FM{displaystyle mathbf {F} _{M}}與淨力FT{displaystyle mathbf {F} _{T}}，帶負電粒子−q{displaystyle -q}會感受到電場力−FE{displaystyle -mathbf {F} _{E}}、磁場力−FM{displaystyle -mathbf {F} _{M}}與淨力−FT{displaystyle -mathbf {F} _{T}}。注意到作用力FT{displaystyle mathbf {F} _{T}}和反作用力−FT{displaystyle -mathbf {F} _{T}}不同線。在本圖內，速度v{displaystyle mathbf {v} }的大小不按比例繪製。

在靜電學裏，場源電荷所產生的電場與試探距離的平方成反比，所以電場力與試探距離的平方成反比。在靜磁學裏，無法獲得類似結果，因為只有移動中的電荷才會產生磁場，而移動中的點電荷無法構成平穩電流，無法用必歐-沙伐定律正確地計算出磁場。在電動力學裏，應用推遲勢概念，可以推導出必歐-沙伐點電荷定律。這定律給出，移動中的場源電荷所產生的電場、磁場與試探距離的平方成反比。所以，電磁力遵守平方反比定律。^[4]:435-440

作用與反作用定律又分为两种版本：强版本和弱版本。这里，第三定律所表述的是「弱版作用與反作用定律」。而「强版作用與反作用定律」，除了弱版作用與反作用定律所要求的以外，还要求作用力和反作用力都作用在同一条直线上。万有引力与静电力都遵守强版作用與反作用定律。可是，在某些状况下，作用力和反作用力并不同线（两作用点的連线）。

設想两个呈平移運動的电荷，其平移速度相同，但并不垂直於两电荷的连线。由於必歐-沙伐點電荷定律与洛伦兹力定律計算出的作用力和反作用力并不同線，这一對電磁力只遵守弱版牛顿第三运动定律。若两移動的电荷，其移動的速度互相垂直，則它們各自感受到的電磁力不遵守弱版牛顿第三运动定律。^{[5]:7[6]:349-351}

基本交互作用

電磁力是四種基本交互作用中的一種，其他的基本交互作用有：

• 
  弱交互作用，影響所有費米子，即所有自旋為半奇數的粒子，而弱交互作用會影響所有費米子，次原子粒子的放射性衰變就是由它引起（在粒子物理學中，弱交互作用和電磁力可以用電弱相互作用來描述）。


• 
  強交互作用，束縛夸克形成核子，束縛核子形成原子核。


• 重力

所有其他的力（例如摩擦力）都是由這些粒子運動帶來的基本交互作用及動量而來。

許多電磁力的現象都是在十九世紀發現^[7]。而日常生活中可以感受到，超過原子尺度以外的現象，除了重力以外，其他都是因為電磁力而造成^[7]。大致上，所有原子之間的交互作用力都可以由帶電的原子核和電子之間的電磁力，以及這些粒子的動量來說明。這包括日常經驗到推或拉一物體的力，可以解釋為身體的分子和物體分子的分子間作用力，所有的化學現象也都是由電磁力而來。

對於原子內作用力和分子間作用力，需要了解的是因電子移動產生動量對應的等效力，以及在相互作用的原子間移動的電子，以及其帶有的動量。當電子越來越密集，因著泡利不相容原理，其最小動量必須變大。物質在分子尺度下的特性（包括其密度）是靠電磁力以及電子上動量交換產生等效力的平衡所決定。

近年來研究發現，在某些狀況下，電磁力和弱核作用力會統一，稱為電弱交互作用，這個發現使得人類距離大統一理論更進一步，科學家阿卜杜勒·薩拉姆、謝爾登·格拉肖以及史蒂文·溫伯格也因此獲頒1979年的諾貝爾物理獎^[8][9]。

相對論下的電磁力

主条目：经典电磁学、電磁場和经典电磁理论的协变形式

在狭义相对论中的電磁交互作用會用一個稱為電磁場張量的二維張量描述：

F=(F00F01F02F03F01F11F12F13F02F21F22F23F03F31F32F33)=(0Ex/cEy/cEz/c−Ex/c0Bz−By−Ey/c−Bz0Bx−Ez/cBy−Bx0){displaystyle mathbf {F} ={begin{pmatrix}F_{00}&F_{01}&F_{02}&F_{03}\F_{01}&F_{11}&F_{12}&F_{13}\F_{02}&F_{21}&F_{22}&F_{23}\F_{03}&F_{31}&F_{32}&F_{33}end{pmatrix}}={begin{pmatrix}0&E_{x}/c&E_{y}/c&E_{z}/c\-E_{x}/c&0&B_{z}&-B_{y}\-E_{y}/c&-B_{z}&0&B_{x}\-E_{z}/c&B_{y}&-B_{x}&0end{pmatrix}}}

以張量方式表示，符合馬克士威方程組的電磁場張量（以CGS制表示）如下：

∂Fαβ∂xα=4πcJβ∂Fαβ∂xγ+∂Fγα∂xβ+∂Fβγ∂xα=ϵμβγgαμ∂Fβγ∂xα=0{displaystyle {partial F^{alpha beta } over {partial x^{alpha }}}={4pi over c}J^{beta }qquad {partial F_{alpha beta } over partial x^{gamma }}+{partial F_{gamma alpha } over partial x^{beta }}+{partial F_{beta gamma } over partial x^{alpha }}=epsilon _{mu beta gamma }g^{alpha mu }{partial F^{beta gamma } over partial x^{alpha }}=0}

方程式還可以用外微分及霍奇對偶寫成更簡潔的形式：

dF=0∗d(∗F)=4πcJ{displaystyle mathrm {d} mathbf {F} =0qquad *mathrm {d} (*mathbf {F} )={frac {4pi }{c}}mathbf {J} }

若方程式為以上的形式，而電磁往外延伸的區域是單連通的，則電磁場可以表示為一個电磁四维势的外導數，电磁四维势是四維勢向量，和經典電磁學的勢有以下的關係：

A=(A0;A1,A2,A3)=(ϕ;A){displaystyle mathbf {A} =(A_{0};A_{1},A_{2},A_{3})=(phi ;mathbf {A} )}

其中

ϕ{displaystyle phi ;}為靜電勢

A{displaystyle mathbf {A} }為向量勢

上述的替換大幅增昇了方程式的解析度，其實上，四維勢向量和電磁張量的關係為：

F=dA=12!∂Aβ∂xα−∂Aα∂xβdxα∧dxβ=12!Fαβdxα∧dxβ{displaystyle mathbf {F} =mathrm {d} mathbf {A} ={frac {1}{2!}}{frac {partial A_{beta }}{partial x^{alpha }}}-{frac {partial A_{alpha }}{partial x^{beta }}}dx^{alpha }land dx^{beta }={frac {1}{2!}}F_{alpha beta }dx^{alpha }land dx^{beta }}

電磁作用可以完全用定義電磁場矢量來表示，這也是現在的電磁作用會用向量表示的原因（在量子處理中，則是向量玻色子）。

在廣義相對論中，在彎曲时空的電磁場和閔可夫斯基時空相近，不過偏微分會用共变导数表示。

量子電動力學

主条目：量子電動力學

在巴巴散射裏，電子與正電子彼此之間倚賴交換光子來實現電磁力。

當進入到原子的尺度時（0.1nm），會發現所有的物質都是由不同的原子構成的，而原子是由不同的原子核與電子構成的，帶負電的電子與帶正電的原子核（由質子與中子構成）經由電磁作用緊密地結合在一起。

但在原子的尺度時，必須用量子化的電磁場來描述。這種描述把兩粒子之間的作用看成是在交換光子。在1950年代，這種描述就已發展得相當完善了，稱作量子電動力學。

量子電動力學是量子力學和電磁學的整合，在電動量子力學中，粒子和場的交互作用和光子有關，光子沒有質量，屬於規範玻色子，光子和帶電粒子之間的交互作用造成了所有電磁學的現象。

根據能量-時間不確定性原理，

ΔEΔt≈ℏ{displaystyle Delta EDelta tapprox hbar }；

其中，ΔE{displaystyle Delta E}、Δt{displaystyle Delta t}分別是能量、時間的不確定性，ℏ{displaystyle hbar }是約化普朗克常數。

一個質量為m{displaystyle m}的媒介粒子最多只能存在T≈ℏ/mc2{displaystyle Tapprox hbar /mc^{2}}時間，否則，能量-時間不確定性原理會被違反。在時間T{displaystyle T}內，這媒介粒子只能移動cT{displaystyle cT}距離，因此，作用力的作用範圍R{displaystyle R}大約為

R≈ℏ/mc{displaystyle Rapprox hbar /mc}。

例如，W玻色子的質量為80GeV，所以，弱力的作用範圍大約為10^-18m。

由於光子的質量為零，電磁力的作用範圍為無窮遠。^[10]:79-80

计量和单位

国际单位制电磁学单位 查 论 编
符号	计量名称	衍生单位	单位	基本单位
I	电流	安培（国际单位制）	A	A（= W/V = C/s）
Q	電荷	库仑	C	A⋅s
U, ΔV, Δφ; E	電壓；電動勢	伏特	V	kg⋅m2⋅s−3⋅A−1（= J/C）
R; Z; X	电阻；阻抗；电抗	歐姆	Ω	kg⋅m2⋅s−3⋅A−2（= V/A）
ρ	电阻率	歐姆米	Ω⋅m	kg⋅m3⋅s−3⋅A−2
P	電功率	瓦特	W	kg⋅m2⋅s−3（= V⋅A）
C	電容	法拉	F	kg−1⋅m−2⋅s4⋅A2（= C/V）
E	電場力	伏特每米	V/m	kg⋅m⋅s−3⋅A−1（= N/C）
D	電位移	库仑每平方米	C/m2	A⋅s⋅m−2
ε	电容率	法拉每米	F/m	kg−1⋅m−3⋅s4⋅A2
χe	電極化率	（无量纲）	–	–
G; Y; B	电导；导纳；电纳	西门子	S	kg−1⋅m−2⋅s3⋅A2（= Ω−1）
κ, γ, σ	电导率	西门子每米	S/m	kg−1⋅m−3⋅s3⋅A2
B	磁感应强度	特斯拉	T	kg⋅s−2⋅A−1（= Wb/m2 = N⋅A−1⋅m−1)
Φ{displaystyle Phi }	磁通量	韦伯	Wb	kg⋅m2⋅s−2⋅A−1（= V⋅s）
H	磁場力	安培每米	A/m	A⋅m−1
L, M	电感	亨利	H	kg⋅m2⋅s−2⋅A−2（= Wb/A = V⋅s/A）
μ	磁导率	亨利每米	H/m	kg⋅m⋅s−2⋅A−2
χ	磁化率	（无量纲）	–	–

參見

• 電磁學


• 電學


• 磁學


• 重力


• 強核作用力


• 弱核作用力


• 量子色動力學


• 電弱統一理論


• 大統一理論

參考資料

1. 
   ^ Ravaioli, Fawwaz T. Ulaby, Eric Michielssen, Umberto. Fundamentals of applied electromagnetics 6th. Boston: Prentice Hall. 2010. ISBN 978-0-13-213931-1.  使用|accessdate=需要含有|url= (帮助)
   


2. 
   ^ Michio Kaku; Jennifer Trainer Thompson. Beyond Einstein: The Cosmic Quest for the Theory of the Universe. Oxford University Press. 1997. ISBN 978-0-19-286196-2. 
   


3. 
   ^ Fred C. Adams. Origins of Existence: How Life Emerged in the Universe. Simon and Schuster. 11 May 2010. ISBN 978-1-4391-3820-5. 
   


4. 
   ^ Griffiths, David J. Introduction to Electrodynamics (3rd ed.). Prentice Hall. 1998. ISBN 0-13-805326-X. 
   


5. 
   ^ Goldstein, Herbert. Classical Mechanics 3rd. United States of America: Addison Wesley. 1980. ISBN 0201657023. 
   


6. 
   ^ Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall, 1998, ISBN 0-13-805326-X 
   


7. 
   ^ ^7.07.1 葉中敏. 人情物理楊振寧. Chinese University Press. 2002: 181–. ISBN 978-962-996-086-5. 
   


8. 
   ^
   S. Bais. The Equations: Icons of knowledge. 2005: 84. ISBN 0-674-01967-9. 
   


9. 
   ^ The Nobel Prize in Physics 1979. The Nobel Foundation. [2008-12-16]. 
   


10. 
    ^ N. A. Jelley. Fundamentals of Nuclear Physics. Cambridge University Press. 22 March 1990. ISBN 978-0-521-26994-0. 
    

查 论 编 物理學的基本相互作用 物理力 强相互作用 弱相互作用 電磁相互作用 引力相互作用 輻射 电磁辐射 重力波 假想的力 第五元素 弱引力猜想

This page is only for reference, If you need detailed information, please check here