挫曲
| ||||||

挫曲(buckling)也稱為屈曲,是一種不穩定的現象,是指細長件在受到壓縮力時,因細長件彎曲變形而造成的結構失效。
理論上,挫曲是因為力学平衡方程式的解出現分岔(解的本質發生改變)所造成的。在受力增加到一定程度之後,物體會出現二種平衡狀態,一種是純壓縮力,另一個是有側向偏移變形的平衡狀態。
挫曲的特點是在結構件中,邊緣承受壓縮應力的元件突然斷裂,而元件失效時的壓應力小於材料可以承受的終極抗壓應力。挫曲的數學分析一般會設法加入方向也是軸向,但和軸有一段位移(偏心)的壓應力,以產生原來理想施力時不會受現的二次彎矩。
當在一元件(例如杆件)上的壓縮負荷增加,多半最後負荷會大到使元件變形不穩定。若負荷繼續加大,會造成明顯,甚至無法預測的變形,可能讓元件完全無法承受負荷。若變形還不是災難性的,元件仍會繼續承受負載。若挫曲的元件是結構件(例如大樓)中的一部份,會由其他的元件來分擔已挫曲元件原來要承受的負載。
目录
1 柱的挫曲
2 相關條目
3 參考資料
4 外部連結
柱的挫曲

承受同心軸向負荷的柱出現挫曲的形變
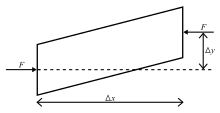
軸向負荷的偏心造成梁元素上的彎矩
柱的有效長度相對於截面積最小迴轉半徑的比例,稱為細長比(slenderness ratio),有時會用希臘字母λ表示。柱的細長比在考慮其挫曲特性時相當重要,以下的值是為了方便使用的近似值。
- 若鐵柱的細長比未超過50,視為短的鐵柱,若細長比介於50到200之間,是中間長度的鐵柱,其特性主要會受材料的強度極限所影響,若細長比超過200,即視為是長的鐵柱,其特性主要會受材料的彈性模數影響。
- 短的水泥柱是指其未支撐長度的細長比小於10的水泥柱,細長比若超過10,即視為是長柱(有時也稱為是細長柱)。
木材若細長比小於10,視為是短柱。中間長度木材和長木材的分界不好決定,有一種定義長木材長度下限的方式其長度需大於最小截面的K倍,K會隨彈性模數影響以及和平行纖維的最大允許壓應力有關,因此會隨木材的品種不同而不同,在許多結構工具書中都會列出不同材料的K值。
若柱子的負載有通過其截面的重心上,稱為軸向負載,若負載未通過重心上,稱為偏心負載。受軸向壓縮力的短柱在挫曲之前,就會因為承受過大的壓縮應力而失效,但受軸向壓縮力的長柱會因挫曲而失效,失效時軸向壓縮應力的影響其實不大,可以忽略。中間長度的柱子在其失效時,是因為壓縮應力及挫曲總和的結果而失效。
數學家萊昂哈德·歐拉在1757年提出了細長理想柱在不挫曲的情形下,可以承受的最大軸向壓縮力。理想柱是指直的、均勻的、沒有初始應力的柱子。其最大負載(有時稱為臨界負載)會使柱處於一個不穩定的平衡狀態,任意小的側向力都會使柱因為挫曲而失效。以下的公式不考慮側向力,不過若將側向力考慮進來,其臨界負載的數值幾乎不會變化。
- F=π2EI(KL)2{displaystyle F={frac {pi ^{2}EI}{(KL)^{2}}}}
其中
F{displaystyle F}為最大臨界力(柱的軸向壓縮力)
E{displaystyle E}為彈性模數
I{displaystyle I}為柱的截面二次轴矩
L{displaystyle L}為柱的未支撐長度
K{displaystyle K}為柱等效長度,其數值視柱子兩側的支撐條件而定:
- 若二端都用插銷連接(可以旋轉),K{displaystyle K}
= 1.0.
- 若二端都固定,無法旋轉,K{displaystyle K}
= 0.50.
- 若一端固定,一端只用插銷連接,K{displaystyle K}
≈ 0.699.
- 若一端固定,另一端可以自由移動,K{displaystyle K}
= 2.0.
- 若二端都用插銷連接(可以旋轉),K{displaystyle K}
KL{displaystyle KL}為柱的等效長度
以上公式中可以看出有關細長柱乘載能力的一些特性。
- 臨界乘載和彈性模數有關,和材料的抗壓強度無關。
- 臨界乘載和截面積的截面二次轴矩成正比。
- 臨界乘載明顯的受邊界支撐條件的影響。邊界支撐條件決定挫曲的形式,也決定挫曲時拐點的位置。細長柱變形時的拐點是在其曲率由正變負或由負變正的位置,也是內彎矩為零的位置。

不同邊界支撐條件下的挫曲情形,四個細長柱材質及形狀都相同,但因為不同的邊界支撐條件,其挫曲情形不同
若重新調整材料分布,增加其截面二次轴矩,就可以提昇臨界乘載。在不增加材料重量的情形下,可以儘可能使材料遠離其截面積的中心軸,就可以提昇臨界乘載,不過也要維持材料有一定的厚度,以免因材料太薄而產生局部的挫曲。若考慮挫曲,相同材料的空心柱比實心柱更可以抵抗挫曲的影響。
由公式中可以看到細長柱的長度對挫曲的影響。若柱的截面積固定,若未支撐的長度加倍,其臨界乘載會變為原來的四分之一。支撐條件也會影響臨界乘載,若支撐條件是完全剛性的(不允許移動及轉動),臨界乘載會是允許轉動支撐條件臨界乘載的四倍。
迴轉半徑定義為截面二次轴矩和截面積商的平方根,因此上式可以重新整理。考慮都是
插銷連接的支撐條件下的尤拉公式,將I用A·r2 取代,尤拉公式會變為以下的式子。
- σ=FA=π2E(ℓ/r)2{displaystyle sigma ={frac {F}{A}}={frac {pi ^{2}E}{(ell /r)^{2}}}}
其中F/A{displaystyle F/A}

由於大部份的結構用柱都是屬於中間長度(臨界乘載除考慮挫曲外,也要考慮強度極限影響),也不可能假設是理想的柱,尤拉公式在原始設計上的實用程式不高。尤拉公式不適用的原因包括幾何上的差異以及材料本身非線性甚至塑性的變形。後來有許多柱的經驗公式可以符合測試的數據,這些公式都具體表現了細長比的概念,再在公式中導入適當的安全係數。其中一個公式是佩里羅伯遜公式,在小曲率的情形下計算臨界乘載。由威廉·约翰·麦夸恩·兰金及Perry Hugesworth Gordon(1899 – 1966)提出的兰金高登公式(Rankine Gordon formula)也是整理實驗結果而來,提出柱的挫曲臨界乘載如下:
- 1Fmax=1Fe+1Fc{displaystyle {frac {1}{F_{max}}}={frac {1}{F_{e}}}+{frac {1}{F_{c}}}}
其中Fe是尤拉臨界乘載,Fc 是最大壓縮乘載,此公式計算的Fmax多半會是保守的估計值。
相關條目
- 佩里羅伯遜公式
- 軌道預力
- 劲化
- 伍德法
- 吉村挫曲
- 歐拉臨界負載
參考資料
外部連結
- The complete theory and example experimental results for long columns are available as a 39-page PDF document at http://lindberglce.com/tech/buklbook.htm
- Laboratory for Physical Modeling of Structures and Photoelasticity (University of Trento, Italy)
- Importance of Buckling Analysis
- https://web.archive.org/web/20100401042249/http://www.midasuser.com.tw/t_support/tech_pds/files/Tech%20Note-Lateral%20Torsional%20Buckling.pdf




Comments
Post a Comment