邏輯閘
基本逻辑门 | |
| BUF | NOT |
| AND | NAND |
| OR | NOR |
| XOR | XNOR |
| IMP | NIMP |
逻辑门是在集成電路上的基本組件。简单的邏輯閘可由晶体管组成。這些晶体管的组合可以使代表两种信号的高低电平在通过它们之后产生高电平或者低电平的信号。高、低电平可以分别代表逻辑上的“真”与“假”或二进制当中的1和0,从而实现邏輯运算。常见的逻辑门包括“與”閘,“或”閘,“非”閘,“異或”閘(也稱:互斥或)等等。
逻辑门是組成數字系統的基本結構,通常组合使用實現更為複雜的邏輯運算。一些廠商通過邏輯門的組合生產一些實用、小型、集成的產品,例如可程式邏輯裝置等。
目录
1 符號表
2 通用邏輯閘
3 参考文献
4 外部連結
符號表
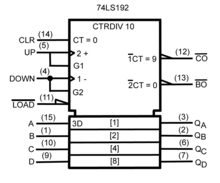
同步型4位元計數器(74LS192) 以ANSI/IEEE Std. 91-1984和IEC Publication 60617-12表示
常用的邏輯閘有兩種常用的表示法,他們皆由ANSI(美國國家標準協會)/IEEE(電機電子工程師學會) Std 91-1984 跟作為其補充的 ANSI/IEEE Std 91a-1991。 「特殊形狀符號」是用過去電路簡圖為基礎以及50年代、60年代MIL-STD-806作衍生;有時也被描述成「軍事」,而這個也反映了它的起源。「IEC矩形國標符號」是以ANSI Y32.14跟一些早期工業用的符號為基礎,再重新由IEEE跟IEC(國際電工委員會)做微調而成;在每個符號中皆可以發現有矩形的外框圍著所代表的字,且相較於舊的表示法,他可以涵蓋更多的邏輯閘[1]。ICE的標準也被轉換成其他的表示法,像是歐洲的EN(歐洲標準委員會)60617-12:1999、英國的BS(由英國標準學會制定) EN 60617-12:1999跟德國的DIN EN 60617-12:1998。
IEEE Std 91-1984跟IEC 60617-12的共同目標是提供一套有系統符號來描述複雜的邏輯功能跟數位電路。這些邏輯的功能相較於AND閘和OR閘更加的複雜,例如中等大小的4位元計數器或大型的微處理器。
IEC 617-12以及接替他的IEC 60617-12沒有很明確的標示出「特殊形狀符號」,但是不可能不使用他們[1]。然而在ANSI/IEEE 91和ANSI/IEEE 91a有提到:「根據IEC刊物第617期的第12部分指出特殊形狀符號不會優先使用,但也沒有和特殊形狀符號有衝突」。IEC 60617-12則包含了相應的說明(在第2.1節):「即使非優先使用,使用其他由國家標準認可的符號-特殊形狀符號,不應被認為和這個標準有衝突。在使用其他特殊形狀符號,以形成複數符號(例如使用如嵌入的符號)不應被鼓勵」。這項妥協方案使的IEEE跟IEC協會各自遵守他們的標準。
第三種表示法比較廣泛用在歐洲,尤其是歐洲的學術界;可以參見"DIN 40700"於德文版的此條目
在1980年代,示意圖成為主要的方式用來設計印刷電路板以及客製化IC(例如邏輯陣列)。而現在,客製化IC和現場可程式邏輯門陣列(field-programmable gate array)通常是用硬體描述語言(Hardware Description Languages)(HDL) such as Verilog or VHDL來做設計。
| 類型 | ANSI及IEEE標準 | IEC標準 | 名称 | 短釋 | 邏輯函數表示 | 真值表 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
AND |  | 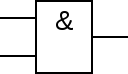 | 「与」门╱「及」閘╱「且」閘 | 所有輸入為高時,才會有高的輸出。 一低出低。 | A⋅B{displaystyle Acdot B}  |
| ||||||||||||||||||
OR | 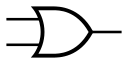 |  | 「或」门/「或」閘 | 所有输入为低时,才会有低的输出。 一高出高。 | A+B{displaystyle A+B,}  |
| ||||||||||||||||||
NOT | 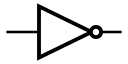 | 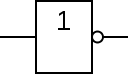 | 「非」门╱反相器╱「反」閘╱逆變器 | 輸入的高低狀態會逆轉。 | A¯{displaystyle {bar {A}}}  |
| ||||||||||||||||||
| 在電子領域中,NOT閘也常常被稱為Inverter。符號的後面常常被稱為泡泡,這個泡泡常被用來表示外部邏輯狀態及內部邏輯狀態(氣泡右側及氣泡左側)的否定關係(1變0、0變1)。在電路圖中,一定需要定義0和1的狀態,通常高電位 = 1 (=5V) , 低電位 = 0(=GND);當然有些時候如果我們要將高電位設為0時,可以直接在電路圖中說明,這稱為直接極性指示,可以參見IEEE Std 91/91A 跟 IEC 60617-12,兩者表示法中泡泡跟電路圖中的說明可以在使用特殊形狀符號及矩形國標符號的電路圖中使用,但是純邏輯電路圖只有泡泡可以使用。 | ||||||||||||||||||||||||
NAND |  | 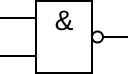 | 「与非」门╱「反及」閘╱「非與」閘╱「反且」閘 | 所有输入为高时,才会有低的输出。 一低出高。 | A⋅B¯{displaystyle {overline {Acdot B}}}  |
| ||||||||||||||||||
NOR | 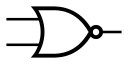 |  | 「或非」门╱「反或」閘╱「非或」閘╱「反或」閘 | 所有输入为低时,才会有高的输出。 一高出低。 | A+B¯{displaystyle {overline {A+B}}}  |
| ||||||||||||||||||
XOR | 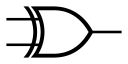 |  | 「异或」门╱「互斥或」閘 | 只有其中一个输入为高时,输出为高;否则为低。 | A⊕B{displaystyle Aoplus B}  |
| ||||||||||||||||||
| XOR閘 (exclusive-OR) 的輸出為1只有當兩個輸入是不同的狀態;反之當兩者輸入為相同的,輸出為0,不論輸入為0或1。如果有超過兩個輸入的話,當輸入端為1的數目是奇數。實際使用上,這些閘是由更基本的邏輯閘組合成的。 | ||||||||||||||||||||||||
XNOR | 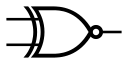 |  | 「同或」门╱「反互斥或」閘╱「互斥反或」閘╱「互斥或非」閘 | 只有其中一个输入为高时,输出为低;否则为高。 | A⊕B¯{displaystyle {overline {Aoplus B}}}  或A⊙B{displaystyle {Aodot B}} |
| ||||||||||||||||||
BUF |  |  | 「是」门╱同相器╱「同」閘╱中繼器 | 輸出一個與輸入相同的高低狀態。 | A{displaystyle A}  |
| ||||||||||||||||||
IMPLY |  |  | 「蘊含」门╱「蘊含」閘 | 如果第一輸入為低時,輸出高,否則輸出與第二輸入相同的高低狀態。 | A→B{displaystyle Ato B}  |
| ||||||||||||||||||
NIMPLY |  |  | 「蘊含非」门╱「蘊含非」閘 | 如果第一輸入為低時,輸出低,否則輸出與第二輸入相反的高低狀態。 | A→B¯{displaystyle {overline {Ato B}}}  或¬(a→b){displaystyle lnot (ato b)} |
| ||||||||||||||||||
通用邏輯閘
查爾斯·桑德斯·皮爾士(1880–81的冬天)指出NOR閘可以單獨使用(或者NAND閘也可以)來產生其他邏輯閘的所有功能,不過他的這個研究一直到1933年才發表。[2]在1913年,Henry M. Sheffer第一個發表NAND閘可以做出全部的功能的證明,也因此NAND閘的邏輯運算有時候也稱為謝費爾豎線(Sheffer stroke);NOR閘有時叫Peirce's arrow。[3]所以這些閘有時候叫做通用邏輯閘
参考文献
^ 1.01.1 Overview of IEEE Standard 91-1984 Explanation of Logic Symbols, Doc. No. SDYZ001A, Texas Instruments Semiconductor Group, 1996
^ Peirce, C. S. (manuscript winter of 1880–81), "A Boolean Algebra with One Constant", published 1933 in Collected Papers v. 4, paragraphs 12–20. Reprinted 1989 in Writings of Charles S. Peirce v. 4, pp. 218-21, Google Preview. See Roberts, Don D. (2009), The Existential Graphs of Charles S. Peirce, p. 131.
^ Hans Kleine Büning; Theodor Lettmann. Propositional logic: deduction and algorithms. Cambridge University Press. 1999: 2. ISBN 978-0-521-63017-7.
外部連結
- 「非」閘Java 模擬
| ||||||||||||||
| ||||||||||||||
|



Comments
Post a Comment