Z轉換

傅里叶变换 Z轉換 傅里叶级数 傅里叶变换 离散傅里叶级数 离散时间傅里叶变换 离散傅里叶变换 快速傅里叶变换 分数傅里叶变换 短时距傅立叶变换 小波变换 離散小波變換 连续小波变换

  關於统计学中的标准Z-分数，請見“標準分數”。關於统计学中的Fisher Z-转换，請見“费雪转换”。

在數學和信号处理中，Z轉換（英语：Z-transform）把一連串離散的實數或複數訊號，從時域轉為复頻域表示。

可以把它认为是拉普拉斯变换的离散时间等价。在时标微积分中会探索它们的相似性

目录

• 
  1 历史
  


• 
  2 定義
  
  
  
  • 
    2.1 双边Z变换
    
  
  
  • 
    2.2 单边Z变换
    
  
  
  • 
    2.3 地球物理学定义
    
  
  
  
  


• 
  3 逆Z变换
  


• 
  4 收敛域
  
  
  
  • 
    4.1 例1（无ROC）
    
  
  
  • 
    4.2 例2（因果ROC）
    
  
  
  • 
    4.3 例3（非因果ROC）
    
  
  
  • 
    4.4 实例结论
    
  
  
  
  


• 
  5 性质
  


• 
  6 常见的Z变换对表
  


• 
  7 与傅里叶级数和傅里叶变换的关系
  


• 
  8 和拉氏变換的關係
  
  
  
  • 
    8.1 双线性变换
    
  
  
  
  


• 
  9 线性常系数差分方程
  
  
  
  • 
    9.1 传递函数
    
  
  
  • 
    9.2 零点和极点
    
  
  
  • 
    9.3 输出响应
    
  
  
  
  


• 
  10 参见
  


• 
  11 参考文献
  


• 
  12 延伸阅读
  


• 
  13 外部链接
  

历史

现在所知的Z变换的基本思想，拉普拉斯就已了解，而1947年W. Hurewicz（英语：Witold Hurewicz）用作求解常系数差分方程的一种容易处理的方式。^[1] 后来由1952年哥伦比亚大学的采样控制组的雷加基尼和查德称其为“Z变换”。^[2][3]

E. I. Jury后来发展并推广了改进或高级Z变换。^[4][5]

Z变换中包含的思想在数学里称作母函数方法，该方法可以追溯到1730年的时候，棣莫弗与概率论结合将其引入。^[6]
从数学的角度，当把数字序列视为解析函数的（洛朗）展开时，Z变换也可以看成是洛朗级数。

定義

像很多积分变换一样，Z变换可以有单边和双边定义。

双边Z变换

双边Z轉換把离散時域信号 x[n] 轉為形式幂级数 X(Z)。

X(z)=Z{x[n]}=∑n=−∞∞x[n]z−n{displaystyle X(z)={mathcal {Z}}{x[n]}=sum _{n=-infty }^{infty }x[n]z^{-n}}

當中 n{displaystyle n} 是整數，z{displaystyle z} 是複數变量，其表示方式為

z=Aejϕ=A(cos⁡ϕ+jsin⁡ϕ){displaystyle z=Ae^{jphi }=A(cos {phi }+jsin {phi }),}

其中 A 为 z 的模，j 为虚数单位，而 ɸ 为幅角（也叫相位角），用弧度表示。

单边Z变换

另外，只对 n ≥ 0 定义的 x[n]，单边Z变换定义为

X(z)=Z{x[n]}=∑n=0∞x[n]z−n.{displaystyle X(z)={mathcal {Z}}{x[n]}=sum _{n=0}^{infty }x[n]z^{-n}.}

在信号处理中，这个定义可以用来计算离散时间因果系统的单位冲激响应。

单边Z变换的一个重要例子是概率母函数，其中 x[n] 部分是离散随机变量取 n 值时的概率，而函数 X(z) 通常写作 X(s)，用 s = z⁻¹ 表示。Z变换的性质（在下面）在概率论背景下有很多有用的解释。

地球物理学定义

地球物理中的Z变换，通常的定义是 z 的幂级数而非 z⁻¹ 的。例如，Robinson、Treitel^[7]和Kanasewich都使用这个惯例。^[8] 地球物理定义为：

X(z)=Z{x[n]}=∑nx[n]zn.{displaystyle X(z)={mathcal {Z}}{x[n]}=sum _{n}x[n]z^{n}.}

这两个定义是等价的；但差分结果会有一些不同。例如，零点和极点的位置移动在单位圆内使用一个定义，在单位圆外用另一个定义。^[7][8]
因此，需要注意特定作者使用的定义。

逆Z变换

逆Z变换为

x[n]=Z−1{X(z)}=12πj∮C⁡X(z)zn−1dz{displaystyle x[n]={mathcal {Z}}^{-1}{X(z)}={frac {1}{2pi j}}oint _{C}X(z)z^{n-1}dz}

其中 C 是完全处于收敛域（ROC）内的包围原点的一个逆时针闭合路径。在 ROC 是因果的情况下（参见例2），这意味着路径 C 必须包围 X(z) 的所有极点。

这个曲线积分的一个特殊情形出现在 C 是单位圆的时候（可以在ROC包含单位圆的时候使用，总能保证 X(z) 是稳定的，即所有极点都在单位圆内）。逆Z变换可以化简为逆离散傅里叶变换：

x[n]=12π∫−π+πX(ejω)ejωndω.{displaystyle x[n]={frac {1}{2pi }}int _{-pi }^{+pi }X(e^{jomega })e^{jomega n}domega .}

有限范围 n 和有限数量的均匀间隔的 z 值的Z变换可以用Bluestein的FFT算法方便地计算。离散时间傅里叶变换 (DTFT)—不要与离散傅里叶变换（DFT）混淆—是通过将 z 限制在位于单位圆上而得到的一种Z变换的特殊情况。

收敛域

收敛域（ROC）是指Z变换的求和收敛的复平面上的点集。

ROC={z:|∑n=−∞∞x[n]z−n|<∞}{displaystyle ROC=left{z:left|sum _{n=-infty }^{infty }x[n]z^{-n}right|<infty right}}

例1（无ROC）

令 x[n] = (0.5)ⁿ。在区间 (−∞, ∞) 上展开 x[n] 成为

x[n]={⋯,0.5−3,0.5−2,0.5−1,1,0.5,0.52,0.53,⋯}={⋯,23,22,2,1,0.5,0.52,0.53,⋯}.{displaystyle x[n]=left{cdots ,0.5^{-3},0.5^{-2},0.5^{-1},1,0.5,0.5^{2},0.5^{3},cdots right}=left{cdots ,2^{3},2^{2},2,1,0.5,0.5^{2},0.5^{3},cdots right}.}

观察上面的和

∑n=−∞∞x[n]z−n→∞.{displaystyle sum _{n=-infty }^{infty }x[n]z^{-n}to infty .}

因此，没有一个 z 值可以满足这个条件。

例2（因果ROC）

ROC用蓝色表示，单位圆用灰色虚点圆表示（外圈者，而 |z| = 0.5 这个圆用虚线圆表示（內圈者）

令 x[n]=0.5nu[n] {displaystyle x[n]=0.5^{n}u[n] }（其中 u 是单位阶跃函数）。在区间 (−∞, ∞) 上展开 x[n] 得到

x[n]={⋯,0,0,0,1,0.5,0.52,0.53,⋯}.{displaystyle x[n]=left{cdots ,0,0,0,1,0.5,0.5^{2},0.5^{3},cdots right}.}

观察这个和

∑n=−∞∞x[n]z−n=∑n=0∞0.5nz−n=∑n=0∞(0.5z)n=11−0.5z−1.{displaystyle sum _{n=-infty }^{infty }x[n]z^{-n}=sum _{n=0}^{infty }0.5^{n}z^{-n}=sum _{n=0}^{infty }left({frac {0.5}{z}}right)^{n}={frac {1}{1-0.5z^{-1}}}.}

最后一个等式来自无穷几何级数，而等式仅在 |0.5z⁻¹| < 1 时成立，可以以 z 为变量写成 |z| > 0.5。因此，收敛域为 |z| > 0.5。在这种情况下，收敛域为复平面“挖掉”原点为中心的半径为 0.5 的圆盘。

例3（非因果ROC）

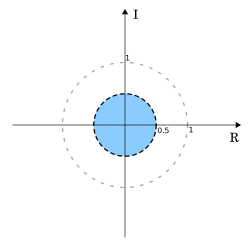
ROC用蓝色表示，单位圆用灰色虚点圆表示（用眼睛看会呈红色），而 |z| = 0.5 这个圆用虚线圆表示

令 x[n]=−(0.5)nu[−n−1] {displaystyle x[n]=-(0.5)^{n}u[-n-1] }（其中 u 是单位阶跃函数）。在区间 (−∞, ∞) 上展开 x[n] 得到

x[n]={⋯,−(0.5)−3,−(0.5)−2,−(0.5)−1,0,0,0,0,⋯}.{displaystyle x[n]=left{cdots ,-(0.5)^{-3},-(0.5)^{-2},-(0.5)^{-1},0,0,0,0,cdots right}.}

观察这个和

∑n=−∞∞x[n]z−n=−∑n=−∞−10.5nz−n=−∑m=1∞(z0.5)m=1−11−0.5−1z=11−0.5z−1{displaystyle sum _{n=-infty }^{infty }x[n]z^{-n}=-sum _{n=-infty }^{-1}0.5^{n}z^{-n}=-sum _{m=1}^{infty }left({frac {z}{0.5}}right)^{m}=1-{frac {1}{1-0.5^{-1}z}}={frac {1}{1-0.5z^{-1}}}}

再次使用无穷几何级数，此等式只在 |0.5⁻¹z| < 1 时成立，可以用 z 为变量写成 |z| < 0.5。因此，收敛域为 |z| < 0.5。在这种情况下，收敛域为中心在原点的半径为 0.5 的圆盘。

本例与上例的不同之处仅在收敛域上。这是意图展示只有变换结果是不够的。

实例结论

实例2和3清楚地表明，当且仅当指定收敛域时，x[n] 的Z变换 X(z) 才是唯一的。画因果和非因果情形的零极点图（英语：pole–zero plot）表明，在这两种情况下收敛域都不包含极点位于 0.5 的情形。这可以拓展到多个极点的情形：收敛域永远不会包含极点。

在例2中，因果系统产生一个包含 |z| = ∞ 的收敛域，而例3中的非因果系统产生包含 |z| = 0 的收敛域。

ROC表示为蓝色圆环 0.5 < |z| < 0.75

在有多个极点的系统中，收敛域可以既不包含 |z| = ∞ 也不包含 |z| = 0。画出的收敛域与一个圆形带。例如，

x[n]=0.5nu[n]−0.75nu[−n−1]{displaystyle x[n]=0.5^{n}u[n]-0.75^{n}u[-n-1]}

的极点为 0.5 与 0.75。收敛域会是 0.5 < |z| < 0.75，不包含原点和无穷大。这样的系统称为混合因果系统，因为它包含一个因果项 (0.5)ⁿu[n] 和一个非因果项 −(0.75)ⁿu[−n−1]。

一个系统的稳定性可以只通过了解收敛域来确定。如果收敛域包含单位圆（即 |z| = 1），那么系统是稳定的。在上述系统中因果系统（例2）是稳定的，因为 |z| > 0.5 包含单位圆。

如果给定一个没有收敛域的Z变换（即模糊的 x[n]），可以确定一个唯一的 x[n] 满足下列：

• 稳定性


• 因果性

如果你要稳定性，收敛域必须包含单位圆；如果你需要一个因果系统，收敛域必须包含无穷大，并且系统函数应为一个右边序列。如果你需要一个非因果系统，那么收敛域必须包含原点，且系统函数为左边序列。如果你既要稳定性，也要因果性，系统函数的所有极点都必须在单位圆内。

可以找到唯一的 x[n]。

性质

Z变换性质

	时域	Z域	证明	收敛域
记法	x[n]=Z−1{X(z)}{displaystyle x[n]={mathcal {Z}}^{-1}{X(z)}}	X(z)=Z{x[n]}{displaystyle X(z)={mathcal {Z}}{x[n]}}		r2<|z|<r1{displaystyle r_{2}<|z|<r_{1}}
線性	a1x1[n]+a2x2[n]{displaystyle a_{1}x_{1}[n]+a_{2}x_{2}[n]}	a1X1(z)+a2X2(z){displaystyle a_{1}X_{1}(z)+a_{2}X_{2}(z)}	X(z)=∑n=−∞∞(a1x1(n)+a2x2(n))z−n=a1∑n=−∞∞x1(n)z−n+a2∑n=−∞∞x2(n)z−n=a1X1(z)+a2X2(z){displaystyle {begin{aligned}X(z)&=sum _{n=-infty }^{infty }(a_{1}x_{1}(n)+a_{2}x_{2}(n))z^{-n}\&=a_{1}sum _{n=-infty }^{infty }x_{1}(n)z^{-n}+a_{2}sum _{n=-infty }^{infty }x_{2}(n)z^{-n}\&=a_{1}X_{1}(z)+a_{2}X_{2}(z)end{aligned}}}	包含 ROC1 ∩ ROC2
时间膨胀	xK[n]={x[r],n=rK0,n≠rK{displaystyle x_{K}[n]={begin{cases}x[r],&n=rK\0,&nnot =rKend{cases}}} r: 整数	X(zK){displaystyle X(z^{K})}	XK(z)=∑n=−∞∞xK(n)z−n=∑r=−∞∞x(r)z−rK=∑r=−∞∞x(r)(zK)−r=X(zK){displaystyle {begin{aligned}X_{K}(z)&=sum _{n=-infty }^{infty }x_{K}(n)z^{-n}\&=sum _{r=-infty }^{infty }x(r)z^{-rK}\&=sum _{r=-infty }^{infty }x(r)(z^{K})^{-r}\&=X(z^{K})end{aligned}}}	R1K{displaystyle R^{frac {1}{K}}}
降采样	x[nK]{displaystyle x[nK]}	1K∑p=0K−1X(z1K⋅e−i2πKp){displaystyle {frac {1}{K}}sum _{p=0}^{K-1}Xleft(z^{tfrac {1}{K}}cdot e^{-i{tfrac {2pi }{K}}p}right)}	ohio-state.edu  或  ee.ic.ac.uk
时移	x[n−k]{displaystyle x[n-k]}	z−kX(z){displaystyle z^{-k}X(z)}	Z{x[n−k]}=∑n=0∞x[n−k]z−n=∑j=−k∞x[j]z−(j+k)j=n−k=∑j=−k∞x[j]z−jz−k=z−k∑j=−k∞x[j]z−j=z−k∑j=0∞x[j]z−jx[β]=0,β<0=z−kX(z){displaystyle {begin{aligned}Z{x[n-k]}&=sum _{n=0}^{infty }x[n-k]z^{-n}\&=sum _{j=-k}^{infty }x[j]z^{-(j+k)}&&j=n-k\&=sum _{j=-k}^{infty }x[j]z^{-j}z^{-k}\&=z^{-k}sum _{j=-k}^{infty }x[j]z^{-j}\&=z^{-k}sum _{j=0}^{infty }x[j]z^{-j}&&x[beta ]=0,beta <0\&=z^{-k}X(z)end{aligned}}}	ROC，除了 k > 0 时 z = 0 和 k < 0 时 z = ∞
Z域的 尺度性质	anx[n]{displaystyle a^{n}x[n]}	X(a−1z){displaystyle X(a^{-1}z)}	Z{anx[n]}=∑n=−∞∞anx(n)z−n=∑n=−∞∞x(n)(a−1z)−n=X(a−1z){displaystyle {begin{aligned}{mathcal {Z}}left{a^{n}x[n]right}&=sum _{n=-infty }^{infty }a^{n}x(n)z^{-n}\&=sum _{n=-infty }^{infty }x(n)(a^{-1}z)^{-n}\&=X(a^{-1}z)end{aligned}}}	|a|r2<|z|<|a|r1{displaystyle |a|r_{2}<|z|<|a|r_{1}}
时间反转	x[−n]{displaystyle x[-n]}	X(z−1){displaystyle X(z^{-1})}	Z{x(−n)}=∑n=−∞∞x(−n)z−n=∑m=−∞∞x(m)zm=∑m=−∞∞x(m)(z−1)−m=X(z−1){displaystyle {begin{aligned}{mathcal {Z}}{x(-n)}&=sum _{n=-infty }^{infty }x(-n)z^{-n}\&=sum _{m=-infty }^{infty }x(m)z^{m}\&=sum _{m=-infty }^{infty }x(m){(z^{-1})}^{-m}\&=X(z^{-1})\end{aligned}}}	1r1<|z|<1r2{displaystyle {tfrac {1}{r_{1}}}<|z|<{tfrac {1}{r_{2}}}}
共轭复数	x∗[n]{displaystyle x^{*}[n]}	X∗(z∗){displaystyle X^{*}(z^{*})}	Z{x∗(n)}=∑n=−∞∞x∗(n)z−n=∑n=−∞∞[x(n)(z∗)−n]∗=[∑n=−∞∞x(n)(z∗)−n]∗=X∗(z∗){displaystyle {begin{aligned}{mathcal {Z}}{x^{*}(n)}&=sum _{n=-infty }^{infty }x^{*}(n)z^{-n}\&=sum _{n=-infty }^{infty }left[x(n)(z^{*})^{-n}right]^{*}\&=left[sum _{n=-infty }^{infty }x(n)(z^{*})^{-n}right]^{*}\&=X^{*}(z^{*})end{aligned}}}
实部	Re⁡{x[n]}{displaystyle operatorname {Re} {x[n]}}	12[X(z)+X∗(z∗)]{displaystyle {tfrac {1}{2}}left[X(z)+X^{*}(z^{*})right]}
虚部	Im⁡{x[n]}{displaystyle operatorname {Im} {x[n]}}	12j[X(z)−X∗(z∗)]{displaystyle {tfrac {1}{2j}}left[X(z)-X^{*}(z^{*})right]}
微分	nx[n]{displaystyle nx[n]}	−zdX(z)dz{displaystyle -z{frac {dX(z)}{dz}}}	Z{nx(n)}=∑n=−∞∞nx(n)z−n=z∑n=−∞∞nx(n)z−n−1=−z∑n=−∞∞x(n)(−nz−n−1)=−z∑n=−∞∞x(n)ddz(z−n)=−zdX(z)dz{displaystyle {begin{aligned}{mathcal {Z}}{nx(n)}&=sum _{n=-infty }^{infty }nx(n)z^{-n}\&=zsum _{n=-infty }^{infty }nx(n)z^{-n-1}\&=-zsum _{n=-infty }^{infty }x(n)(-nz^{-n-1})\&=-zsum _{n=-infty }^{infty }x(n){frac {d}{dz}}(z^{-n})\&=-z{frac {dX(z)}{dz}}end{aligned}}}
卷积	x1[n]∗x2[n]{displaystyle x_{1}[n]*x_{2}[n]}	X1(z)X2(z){displaystyle X_{1}(z)X_{2}(z)}	Z{x1(n)∗x2(n)}=Z{∑l=−∞∞x1(l)x2(n−l)}=∑n=−∞∞[∑l=−∞∞x1(l)x2(n−l)]z−n=∑l=−∞∞x1(l)[∑n=−∞∞x2(n−l)z−n]=[∑l=−∞∞x1(l)z−l][∑n=−∞∞x2(n)z−n]=X1(z)X2(z){displaystyle {begin{aligned}{mathcal {Z}}{x_{1}(n)*x_{2}(n)}&={mathcal {Z}}left{sum _{l=-infty }^{infty }x_{1}(l)x_{2}(n-l)right}\&=sum _{n=-infty }^{infty }left[sum _{l=-infty }^{infty }x_{1}(l)x_{2}(n-l)right]z^{-n}\&=sum _{l=-infty }^{infty }x_{1}(l)left[sum _{n=-infty }^{infty }x_{2}(n-l)z^{-n}right]\&=left[sum _{l=-infty }^{infty }x_{1}(l)z^{-l}right]!!left[sum _{n=-infty }^{infty }x_{2}(n)z^{-n}right]\&=X_{1}(z)X_{2}(z)end{aligned}}}	包含 ROC1 ∩ ROC2
互相关	rx1,x2=x1∗[−n]∗x2[n]{displaystyle r_{x_{1},x_{2}}=x_{1}^{*}[-n]*x_{2}[n]}	Rx1,x2(z)=X1∗(1z∗)X2(z){displaystyle R_{x_{1},x_{2}}(z)=X_{1}^{*}({tfrac {1}{z^{*}}})X_{2}(z)}		包含 X1(1z∗){displaystyle X_{1}({tfrac {1}{z^{*}}})} 与 X2(z){displaystyle X_{2}(z)} 的ROC的交集
一阶差分	x[n]−x[n−1]{displaystyle x[n]-x[n-1]}	(1−z−1)X(z){displaystyle (1-z^{-1})X(z)}		包含 X1(z) 与 z ≠ 0 的ROC的交集
累积	∑k=−∞nx[k]{displaystyle sum _{k=-infty }^{n}x[k]}	11−z−1X(z){displaystyle {frac {1}{1-z^{-1}}}X(z)}	∑n=−∞∞∑k=−∞nx[k]z−n=∑n=−∞∞(x[n]+⋯+x[−∞])z−n=X[z](1+z−1+z−2+⋯)=X[z]∑j=0∞z−j=X[z]11−z−1{displaystyle {begin{aligned}sum _{n=-infty }^{infty }sum _{k=-infty }^{n}x[k]z^{-n}&=sum _{n=-infty }^{infty }(x[n]+cdots +x[-infty ])z^{-n}\&=X[z]left(1+z^{-1}+z^{-2}+cdots right)\&=X[z]sum _{j=0}^{infty }z^{-j}\&=X[z]{frac {1}{1-z^{-1}}}end{aligned}}}
乘法	x1[n]x2[n]{displaystyle x_{1}[n]x_{2}[n]}	1j2π∮C⁡X1(v)X2(zv)v−1dv{displaystyle {frac {1}{j2pi }}oint _{C}X_{1}(v)X_{2}({tfrac {z}{v}})v^{-1}mathrm {d} v}		-

帕塞瓦尔定理

∑n=−∞∞x1[n]x2∗[n]=1j2π∮C⁡X1(v)X2∗(1v∗)v−1dv{displaystyle sum _{n=-infty }^{infty }x_{1}[n]x_{2}^{*}[n]quad =quad {frac {1}{j2pi }}oint _{C}X_{1}(v)X_{2}^{*}({tfrac {1}{v^{*}}})v^{-1}mathrm {d} v}

初值定理：如果 x[n] 为因果的，那么

x[0]=limz→∞X(z).{displaystyle x[0]=lim _{zto infty }X(z).}

终值定理：如果 (z−1)X(z) 的极点在单位圆内，则

x[∞]=limz→1(z−1)X(z).{displaystyle x[infty ]=lim _{zto 1}(z-1)X(z).}

常见的Z变换对表

这里：

u:n↦u[n]={1,n≥00,n<0{displaystyle u:nmapsto u[n]={begin{cases}1,&ngeq 0\0,&n<0end{cases}}}

是单位阶跃函数而

δ:n↦δ[n]={1,n=00,n≠0{displaystyle delta :nmapsto delta [n]={begin{cases}1,&n=0\0,&nneq 0end{cases}}}

是离散时间单位冲激函数。两者通常都不认为是真正的函数，但由于它们的不连续性把它们看成是分布（它们在 n = 0 处的值通常无关紧要，除非在处理离散时间的时候，它们会变成衰减离散级数；在本章节中对连续和离散时间域，都在 n = 0 处取 1，否则不能使用下表中收敛域一栏的内容）。同时列出两个“函数”，使得（在连续时间域）单位阶跃函数是单位冲激函数的积分，或（在离散时间域）单位阶跃函数是单位冲激函数的求和，因此要令他们的值在 n = 0 处为 1。

	信号，x[n]{displaystyle x[n]}	Z变换，X(z){displaystyle X(z)}	ROC
1	δ[n]{displaystyle delta [n]}	1	所有 z
2	δ[n−n0]{displaystyle delta [n-n_{0}]}	z−n0{displaystyle z^{-n_{0}}}	z≠0{displaystyle zneq 0}
3	u[n]{displaystyle u[n],}	11−z−1{displaystyle {frac {1}{1-z^{-1}}}}	|z|>1{displaystyle |z|>1}
4	e−αnu[n]{displaystyle e^{-alpha n}u[n]}	11−e−αz−1{displaystyle 1 over 1-e^{-alpha }z^{-1}}	|z|>e−α{displaystyle |z|>e^{-alpha },}
5	−u[−n−1]{displaystyle -u[-n-1]}	11−z−1{displaystyle {frac {1}{1-z^{-1}}}}	|z|<1{displaystyle |z|<1}
6	nu[n]{displaystyle nu[n]}	z−1(1−z−1)2{displaystyle {frac {z^{-1}}{(1-z^{-1})^{2}}}}	|z|>1{displaystyle |z|>1}
7	−nu[−n−1]{displaystyle -nu[-n-1],}	z−1(1−z−1)2{displaystyle {frac {z^{-1}}{(1-z^{-1})^{2}}}}	|z|<1{displaystyle |z|<1}
8	n2u[n]{displaystyle n^{2}u[n]}	z−1(1+z−1)(1−z−1)3{displaystyle {frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}}	|z|>1{displaystyle |z|>1,}
9	−n2u[−n−1]{displaystyle -n^{2}u[-n-1],}	z−1(1+z−1)(1−z−1)3{displaystyle {frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}}	|z|<1{displaystyle |z|<1,}
10	n3u[n]{displaystyle n^{3}u[n]}	z−1(1+4z−1+z−2)(1−z−1)4{displaystyle {frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}}	|z|>1{displaystyle |z|>1,}
11	−n3u[−n−1]{displaystyle -n^{3}u[-n-1]}	z−1(1+4z−1+z−2)(1−z−1)4{displaystyle {frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}}	|z|<1{displaystyle |z|<1,}
12	anu[n]{displaystyle a^{n}u[n]}	11−az−1{displaystyle {frac {1}{1-az^{-1}}}}	|z|>|a|{displaystyle |z|>|a|}
13	−anu[−n−1]{displaystyle -a^{n}u[-n-1]}	11−az−1{displaystyle {frac {1}{1-az^{-1}}}}	|z|<|a|{displaystyle |z|<|a|}
14	nanu[n]{displaystyle na^{n}u[n]}	az−1(1−az−1)2{displaystyle {frac {az^{-1}}{(1-az^{-1})^{2}}}}	|z|>|a|{displaystyle |z|>|a|}
15	−nanu[−n−1]{displaystyle -na^{n}u[-n-1]}	az−1(1−az−1)2{displaystyle {frac {az^{-1}}{(1-az^{-1})^{2}}}}	|z|<|a|{displaystyle |z|<|a|}
16	n2anu[n]{displaystyle n^{2}a^{n}u[n]}	az−1(1+az−1)(1−az−1)3{displaystyle {frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}}	|z|>|a|{displaystyle |z|>|a|}
17	−n2anu[−n−1]{displaystyle -n^{2}a^{n}u[-n-1]}	az−1(1+az−1)(1−az−1)3{displaystyle {frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}}	|z|<|a|{displaystyle |z|<|a|}
18	cos⁡(ω0n)u[n]{displaystyle cos(omega _{0}n)u[n]}	1−z−1cos⁡(ω0)1−2z−1cos⁡(ω0)+z−2{displaystyle {frac {1-z^{-1}cos(omega _{0})}{1-2z^{-1}cos(omega _{0})+z^{-2}}}}	|z|>1{displaystyle |z|>1}
19	sin⁡(ω0n)u[n]{displaystyle sin(omega _{0}n)u[n]}	z−1sin⁡(ω0)1−2z−1cos⁡(ω0)+z−2{displaystyle {frac {z^{-1}sin(omega _{0})}{1-2z^{-1}cos(omega _{0})+z^{-2}}}}	|z|>1{displaystyle |z|>1}
20	ancos⁡(ω0n)u[n]{displaystyle a^{n}cos(omega _{0}n)u[n]}	1−az−1cos⁡(ω0)1−2az−1cos⁡(ω0)+a2z−2{displaystyle {frac {1-az^{-1}cos(omega _{0})}{1-2az^{-1}cos(omega _{0})+a^{2}z^{-2}}}}	|z|>|a|{displaystyle |z|>|a|}
21	ansin⁡(ω0n)u[n]{displaystyle a^{n}sin(omega _{0}n)u[n]}	az−1sin⁡(ω0)1−2az−1cos⁡(ω0)+a2z−2{displaystyle {frac {az^{-1}sin(omega _{0})}{1-2az^{-1}cos(omega _{0})+a^{2}z^{-2}}}}	|z|>|a|{displaystyle |z|>|a|}

与傅里叶级数和傅里叶变换的关系

对于区域 |z|=1（称为单位圆）内的 z 值，我们可以通过定义 z=e^jω 来用单一实变量的函数来表示该变换。于是双边变换就简化为了傅里叶级数：

∑n=−∞∞x[n] z−n=∑n=−∞∞x[n] e−jωn,{displaystyle sum _{n=-infty }^{infty }x[n] z^{-n}=sum _{n=-infty }^{infty }x[n] e^{-jomega n},}

(Eq.1)

也被称作 x[n] 序列的离散时间傅里叶变换（DTFT）。这个以 2π 为周期的函数是傅里叶变换的周期性求和（英语：periodic summation），这使得它成为广泛使用的分析工具。要理解这一点，令 X(f) 为任意函数 x(t) 的傅里叶变换，该函数以某个间隔 T 采样就与 x[n] 序列相等。于是 x[n] 序列的DTFT可以写作：

∑n=−∞∞x(nT)⏞x[n] e−j2πfnT⏟DTFT=1T∑k=−∞∞X(f−k/T).{displaystyle underbrace {sum _{n=-infty }^{infty }overbrace {x(nT)} ^{x[n]} e^{-j2pi fnT}} _{text{DTFT}}={frac {1}{T}}sum _{k=-infty }^{infty }X(f-k/T).}

若T的單位是秒，f{displaystyle textstyle f}的單位即為赫兹。比較兩個數列可得 ω=2πfT{displaystyle textstyle omega =2pi fT} 為标准化频率（英语：Normalized frequency (digital signal processing)#Alternative normalizations），單位是radians per sample。數值ω=2π對應f=1T{displaystyle textstyle f={frac {1}{T}}} Hz. ，而且在替換 f=ω2πT,{displaystyle textstyle f={frac {omega }{2pi T}},}後，  Eq.1可以表示為傅里叶变换X(•):

∑n=−∞∞x[n] e−jωn=1T∑k=−∞∞X(ω2πT−kT)⏟X(ω−2πk2πT).{displaystyle sum _{n=-infty }^{infty }x[n] e^{-jomega n}={frac {1}{T}}sum _{k=-infty }^{infty }underbrace {Xleft({tfrac {omega }{2pi T}}-{tfrac {k}{T}}right)} _{Xleft({frac {omega -2pi k}{2pi T}}right)}.}

若數列x(nT)表示线性时不变系统的冲激响应，這些函數也稱為频率响应，當x(nT)是週期性數列，其DTFT在一或多個共振頻率發散，在其他頻率均為零。這一般會用在共振頻率，振幅可變的狄拉克δ函数表示。因為其週期性，只會有有限個振幅，可以用較簡單許多的离散傅里叶变换來計算。（參照離散傅立葉變換#周期性）

和拉氏变換的關係

双线性变换

双线性变换可以用在連續時間濾波器（用拉氏域表示）和離散時間濾波器（用Z域表示）之間的轉換，其轉換關係如下：

s=2T(z−1)(z+1){displaystyle s={frac {2}{T}}{frac {(z-1)}{(z+1)}}}

將一個拉氏域的函數H(s){displaystyle H(s)}轉換為Z域下的H(z){displaystyle H(z)}，或是

z=2+sT2−sT{displaystyle z={frac {2+sT}{2-sT}}}

從Z域轉換到拉氏域。藉由双线性变换，複數的s平面（拉氏变換）可以映射到複數的z平面（Z轉換）。這個轉換是非線性的，可以將S平面的整個jΩ軸映射到Z平面的单位圆內。因此，傅立葉變換（在jΩ axis計算的拉氏變換）變成離散時間傅立葉變換，前提是假設其傅立葉變換存在，也就是拉氏变換的收斂區域包括jΩ軸。

线性常系数差分方程

线性常系数差分（LCCD）方程是基于自回归滑动平均的线性系统表达形式。

∑p=0Ny[n−p]αp=∑q=0Mx[n−q]βq{displaystyle sum _{p=0}^{N}y[n-p]alpha _{p}=sum _{q=0}^{M}x[n-q]beta _{q}}

上面等式两边可以同时除以 α₀，如果非零，正规化 α₀ = 1，LCCD方程可以写成

y[n]=∑q=0Mx[n−q]βq−∑p=1Ny[n−p]αp.{displaystyle y[n]=sum _{q=0}^{M}x[n-q]beta _{q}-sum _{p=1}^{N}y[n-p]alpha _{p}.}

LCCD方程的这种形式有利于更加明确“当前”输出 y[n] 是过去输出 y[n−p]、当前输入 x[n] 与之前输入 x[n−q] 的一个函数。

传递函数

对上述方程去Z变换（使用线性和时移法则）得到

Y(z)∑p=0Nz−pαp=X(z)∑q=0Mz−qβq{displaystyle Y(z)sum _{p=0}^{N}z^{-p}alpha _{p}=X(z)sum _{q=0}^{M}z^{-q}beta _{q}}

整理结果

H(z)=Y(z)X(z)=∑q=0Mz−qβq∑p=0Nz−pαp=β0+z−1β1+z−2β2+⋯+z−MβMα0+z−1α1+z−2α2+⋯+z−NαN.{displaystyle H(z)={frac {Y(z)}{X(z)}}={frac {sum _{q=0}^{M}z^{-q}beta _{q}}{sum _{p=0}^{N}z^{-p}alpha _{p}}}={frac {beta _{0}+z^{-1}beta _{1}+z^{-2}beta _{2}+cdots +z^{-M}beta _{M}}{alpha _{0}+z^{-1}alpha _{1}+z^{-2}alpha _{2}+cdots +z^{-N}alpha _{N}}}.}

零点和极点

由代数基本定理得知分子有 M 个根（对应于 H 的零点）和分母有 N 个根（对应于极点）。用极点和零点重新整理传递函数为

H(z)=(1−q1z−1)(1−q2z−1)⋯(1−qMz−1)(1−p1z−1)(1−p2z−1)⋯(1−pNz−1){displaystyle H(z)={frac {(1-q_{1}z^{-1})(1-q_{2}z^{-1})cdots (1-q_{M}z^{-1})}{(1-p_{1}z^{-1})(1-p_{2}z^{-1})cdots (1-p_{N}z^{-1})}}}

其中 q_k 为 k 阶零点，p_k 为 k 阶极点。零点和极点通常是复数，当在复平面（z平面）作图时称为零极点图（英语：pole–zero plot）。

此外，在 z = 0 和 z = ∞ 也可能存在零点和极点。如果我们把这些极点和零点以及高阶零点和极点考虑在内的話，零点和极点的数目总会相等。

通过对分母因式分解，可以使用部分分式分解可以转换回时域。这样做会导出系统的冲激响应和线性常系数差分方程。

输出响应

如果一个系统 H(z) 由信号 X(z) 驱动，那么输出为 Y(z) = H(z)X(z)。通过对 Y(z) 部分分式分解并取逆Z变换可以得到输出 y[n]。在实际运用中，在分式分解 Y(z)z{displaystyle {frac {Y(z)}{z}}} 之后再乘 z 产生 Y(z) 的一个形式（含有很容易计算逆Z变换的项）往往很有用。

参见

• 高级Z变换


• 双线性变换


• 
  差分方程（遞迴關係式）


• 离散卷积


• 离散时间傅里叶变换


• 有限脉冲响应


• 形式幂级数


• 拉普拉斯变换


• 洛朗级数


• 概率母函数


• Star变换（英语：Star transform）


• Zak变换（英语：Zak transform）


• ζ函数正规化（英语：Zeta function regularization）

参考文献

1. 
   ^ E. R. Kanasewich. Time sequence analysis in geophysics 3rd. University of Alberta. 1981: 185–186. ISBN 978-0-88864-074-1. 
   


2. 
   ^ J. R. Ragazzini and L. A. Zadeh. The analysis of sampled-data systems. Trans. Am. Inst. Elec. Eng. 1952, 71 (II): 225–234. 
   


3. 
   ^ Cornelius T. Leondes. Digital control systems implementation and computational techniques. Academic Press. 1996: 123. ISBN 978-0-12-012779-5. 
   


4. 
   ^
   Eliahu Ibrahim Jury. Sampled-Data Control Systems. John Wiley & Sons. 1958. 
   


5. 
   ^
   Eliahu Ibrahim Jury. Theory and Application of the Z-Transform Method. Krieger Pub Co. 1973. ISBN 0-88275-122-0. 
   


6. 
   ^
   Eliahu Ibrahim Jury. Theory and Application of the Z-Transform Method. John Wiley & Sons. 1964: 1. 
   


7. 
   ^ ^7.07.1
   Enders A. Robinson, Sven Treitel. Digital Imaging and Deconvolution: The ABCs of Seismic Exploration and Processing Digital Imaging and Deconvolution: The ABCs of Seismic Exploration and Processing. SEG Books. 2008: 163, 375–376. ISBN 9781560801481. 
   


8. 
   ^ ^8.08.1
   E. R. Kanasewich. Time Sequence Analysis in Geophysics. University of Alberta. 1981: 186, 249. ISBN 9780888640741. 
   

延伸阅读

• Refaat El Attar, Lecture notes on Z-Transform, Lulu Press, Morrisville NC, 2005. ISBN 978-1-4116-1979-1.


• Ogata, Katsuhiko, Discrete Time Control Systems 2nd Ed, Prentice-Hall Inc, 1995, 1987. ISBN 978-0-13-034281-2.


• Alan V. Oppenheim and Ronald W. Schafer (1999). Discrete-Time Signal Processing, 2nd Edition, Prentice Hall Signal Processing Series. ISBN 978-0-13-754920-7.

外部链接

• 
  Hazewinkel, Michiel (编), Z-transform, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
  


• Z-Transform table of some common Laplace transforms


• Mathworld's entry on the Z-transform


• Z-Transform threads in Comp.DSP


• Z-Transform Module by John H. Mathews


• A graphic of the relationship between Laplace transform s-plane to Z-plane of the Z transform

查 论 编 数字信号处理 理论 信号检测理论 离散信号 估计理论 采样定理 子领域 音频信号处理 数字图像处理 语音处理 统计信号处理（英语：Statistical signal processing） 方法 高级Z变换 雙線性轉換 离散傅里叶变换（DFT） 離散分數傅立葉轉換（DFFT） 离散时间傅里叶变换（DTFT） 冲激不变法 匹配Z变换方法 Z轉換 Zak变换（英语：Zak transform） 取樣 混疊 抗混叠滤波器 降采样 奈奎斯特率（英语：Nyquist rate） / 频率 过采样 量化 取样率 欠采样（英语：Undersampling） 升採樣

查 论 编 控制理论 領域分支 自适应控制 控制理论 數位控制 能量成型控制 模糊控制 混合（英语：Hybrid computer）控制 智能控制 模型預測控制 多變數控制 神经系统控制 非線性控制（英语：Nonlinear control） 最优控制 实时计算 鲁棒控制 隨機控制 系統特性 時域 頻域 波德圖 奈奎斯特图 尼柯尔斯图 方塊圖 閉迴路傳遞函數 可控制性 傅里叶变换 频率响应 拉普拉斯变换 负反馈 可觀測性 性能 正回饋 根軌跡圖法 伺服機構 信号流图 状态空间 穩定性理論（英语：Stability theory） 穩態（英语：Steady State）分析及設計 系统动力学 传递函数 數位控制 離散時間信號 数字信号处理 量化 實時軟體 取樣資料 系統識別 Z轉換 進階理論 人工神经网络 係數圖法（英语：Coefficient diagram method） 控制重構 分佈式參數系統 分數階控制 模糊逻辑 H-infinity迴路成形 漢克爾奇異值 卡尔曼滤波 Krener's theorem（英语：Krener's theorem） 最小二乘法 李雅普诺夫稳定性 小迴路回授 知覺控制理論（英语：Perceptual control theory） 狀態觀測器 向量控制 控制器 嵌入式控制器 超前-滞后补偿器 数控机床 PID控制器 可编程逻辑控制器 控制應用 Automation and Remote Control（英语：Automation and Remote Control） 分散式控制系統（英语：Distributed Control System） 电动机 工業控制系統（英语：Industrial Control Systems） 机械电子学 運動控制 过程控制 机器人学 数据采集与监控系统（SCADA）

This page is only for reference, If you need detailed information, please check here