功

建議将动能定理併入本條目或章節。（討論）

功（英语：work），也叫机械功，是物理学中表示力对位移的累积的物理量，指从一种物理系统到另一种物理系统的能量转变，尤其是指通过使物体朝向力的方向移动的力的作用下能量的转移。与机械能相似的是，功也是标量，国际单位制单位为焦耳。

球员对球作正功，使其动能增加。
通用符號：W
SI單位：J（焦耳）
基本公式：W = F×D，W = τθ

“功”一词最初是法国数学家贾斯帕-古斯塔夫·科里奥利创造的。^[1]

由动能定理，若一个外力作用于一物体使之动能从E_k0增至E_k，那么，此力所作的机械功为：

W=ΔEk=Ek−Ek0=12m(v2−v02){displaystyle W=Delta E_{rm {k}}=E_{rm {k}}-E_{mathrm {k} 0}={tfrac {1}{2}}m(v^{2}-v_{0}^{2}),!}^[2]

其中m是物体的质量，v是物体的速度。

机械功就是力与位移的內積：

W=F→⋅d→{displaystyle W={vec {F}}cdot {vec {d}}}^[3]

若力与位移的夹角小于直角，则机械功为正，亦称为力作正功。若力与位移的夹角大于直角，则机械功为负，或力作负功，或物体克服力作功。

若力的方向与位移方向垂直，则此力不作功：^[3]

W=0{displaystyle W=0}

舉例來說：一個10牛頓（F=10 N）的力沿著點移動兩公尺（D=2 m），那麼它所作的功為W=10 N·2 m = 20 N m = 20 J，這相當於從地面舉起1公斤重的物體到頭部所作的功。

注意：若重量加倍，距離不變；或是重量不變，距離加倍，其所作的功皆為例題的兩倍。

1.能量、儲存、轉換→用功作為轉換方式及過程
2.對物體作功會轉換成能量

     功

動能→→→位能

 A        B

目录

• 
  1 简介
  


• 
  2 单位
  


• 
  3 功與能
  
  
  
  • 
    3.1 只有机械能时的情况
    
  
  
  
  


• 
  4 約束力
  


• 
  5 数学计算
  
  
  
  • 
    5.1 轉矩和轉動
    
  
  
  • 
    5.2 力与位移
    
  
  
  • 
    5.3 力矩
    
  
  
  
  


• 
  6 功與動能
  
  
  
  • 
    6.1 概述
    
  
  
  
  


• 
  7 注释
  


• 
  8 参考
  

简介

即使存在力，也可能没有作功。例如，在匀速圆周运动中，向心力没有作功，因为做圆周运动的物体的动能没有发生变化。同样的，桌上的一本书，尽管桌对书有支持力，但因没有位移而没有作功。

单位

国际单位制中功的单位为焦耳（J）。焦耳被定义为用1牛顿的力对一物体使其发生1米的位移所做的机械功的大小。量纲相同的单位牛·米有时也使用，但是一般牛·米用于力矩，使其跟功和能区别开。

非国际单位制单位包括尔格、英尺·磅、千瓦时（kW•h）、大氣壓力、马力时（HP•h）。而由於具有相同的物理量─熱能，偶爾會見到以熱量熱能形式表示的測量單位，如：卡路里（cal）、BTU等。

功與能

功與能息息相關，根據系統能量的守恆，內部總能量的變化等於添加的熱能加上环境对系統所作的功。見熱力學第一定律。

dE=δQ+δW{displaystyle mathrm {d} E=delta Q+delta W}

只有机械能时的情况

1.保守力作功使「存」在物體中的位能釋放出來，亦即保守力作功等於負的位能變：

W=−ΔU{displaystyle W=-Delta U}

2.非保守力作功時，若有保守力作負功則優先化為位能，剩下的功才化為物體的動能，即非保守力作功等於總力學能（動能+位能）變：

W=ΔE=ΔEk+ΔU{displaystyle W=Delta E=Delta E_{rm {k}}+Delta U}

3.綜合以上兩點，一物體所受的合力包含了保守力與非保守力，非保守力使總力學能變，而保守力將之部份化為位能，二者相加，即合力作功等於動能變：

W=ΔEk{displaystyle W=Delta E_{rm {k}}}

根據這些公式證明功是與作用力相關的能量，所以作功是能被測量的，是一種具有物理單位的能量。

上面所討論的作功、能量原理也适用于非机械能，例如電器和能源等，其原理是相同的。

約束力

约束力决定了系统中物件的位移，將其限制在範圍內（以斜面加重力為例，當物體受到無法再伸長的緊繩約束使其不能再下滑，物體就會卡在斜面上）。它消除了在該方向上所有的位移，即物體平行此力的速度被約束為0，因此約束力不對系統作功。

例如：用一根绳子系上一个小球做匀速圆周运动，小球会受到来自绳子，方向指向圆心的一个向心力。这个力的方向和球速度的方向垂直，所以这个力不作功（W=0）。又如桌上有一本书，施加外力会使书在桌面上移动。如果再对书施加一个垂直的力（实际上书受到的重力和支持力就属于这个力），和其欲移动之方向垂直，则此约束力（施加的垂直力）不作功。

磁场中的带电粒子受到磁力（洛伦兹力）的大小为F = qv×B，其中q为电荷，v是粒子速度，而B为磁场强度。外积结果恆垂直于兩原向量，因此F⊥v。而两垂直向量的內积恆零，因此磁力作的功W = F · v = 0。磁力可改变此粒子运动的方向，但是永远无法改变运动速度（也就是動能）。

数学计算

對於一移動的物體而言，作功量/時間可以從距離/時間（即速度V）來計算。因此，在任何時刻，力所作的功率（焦耳/秒、瓦），其值為力的純量積（矢量）和作用點上的速度矢量。力的純量積和速度被歸類為瞬時功率。

而正如速度可能會隨著時間的推移以獲得更長的距離，同一條路徑上的總功率也同樣是作用點沿著同一條路徑上之瞬時功率的時間積分的總和。

功是指質點受外力作用位移而產生的量，當質點移動時，它沿著曲線X和速度V在所有的時間t。少量的功δW發生在瞬時時間δt能夠寫成：

δW=F⋅vδt,{displaystyle delta W=mathbf {F} cdot mathbf {v} delta t,}其中F.v是在δt內的瞬時功率，這些少量功的總合超過該質點運動位移所產生的功量。

W=∫t1t2F⋅vdt=∫t1t2F⋅dxdtdt=∫CF⋅dx,{displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt=int _{t_{1}}^{t_{2}}mathbf {F} cdot {tfrac {dmathbf {x} }{dt}}dt=int _{C}mathbf {F} cdot dmathbf {x} ,}

其中C的位移是從x（t₁）到x（t₂），計算質點位移的積分。

如果力的方向總是沿著這條線，力的大小為F，那麼此積分可簡化為：

W=∫CFds{displaystyle W=int _{C}Fds}

其中s是沿著直線的位移，假設F固定，且沿著此直線，則此積分可進一步簡化成：

W=∫CFds=F∫Cds=Fd{displaystyle W=int _{C}Fds=Fint _{C}ds=Fd}

其中d是質點沿著直線前進的距離。

此計算可歸納為恆定力並非延著線而是沿著質點。在此情況下點的乘積F·dx = Fcosθdx，其中θ是力矢量和運動方向之間的角度。即：

W=∫CF⋅dx=Fdcos⁡θ{displaystyle W=int _{C}mathbf {F} cdot dmathbf {x} =Fdcos theta }。

一般常見的情況，施加的力和速度矢量對身體成90^。角（中央力朝下身體繞一圓圈運動），由於cos90^。為0，所以不作功。因此可以延伸至重力對於星球在圓形軌道上運動不作功（此為理想情況，一般情況下軌道略呈橢圓形）。

此外身體作一等速圓周運動受到機械外力作用時，作的功也為0，就像在一理想情況之無摩擦力的離心機中作等速圓周運動一般。

計算功在時間和力作用在一直線路徑上的數值只適用在最簡單的情況下，如上文所述。如果力會變化，或身體延曲線方向移動，物體可能轉動甚至並非剛性物體，那麼其所作的功只和作用力的角度、路徑有關，並且只有部分的力平行在作用點上形成的速度才作功
（相同方向為正，反方向為負值），此處的力可以被描述為純量或是切線分量的純量。（Fcosθ，其中θ是力和速度之間的夾角）。

至於功最普遍的定義如下：力作功是其延著作用點上的路徑之切線分量的純量也就是線性積分。

轉矩和轉動

轉矩是從相等但方向相反的力作用於剛性體上兩個不同的點所形成。這些力總合為零，但它會對物體影響形成轉矩Τ，計算作功形成的轉矩公式為：

δW=T⋅ω→δt,{displaystyle delta W=mathbf {T} cdot {vec {omega }}delta t,}，其中T.ω是作用在時間點δt上。這些少量的功之合大於剛性體運動軌跡所產生的功。

W=∫t1t2T⋅ω→dt.{displaystyle W=int _{t_{1}}^{t_{2}}mathbf {T} cdot {vec {omega }}dt.}，此積分是計算剛體延軌跡運動與時間變化的角速度ω，可以說與運動的路徑息息相關。

如果角速度矢量保持恆定的方向，那麼可以寫成：

ω→=ϕ˙S,{displaystyle {vec {omega }}={dot {phi }}mathbf {S} ,}，其中φ為轉動角度，單位矢量S。在此情況下，功的轉矩可寫成：

W=∫t1t2T⋅ω→dt=∫t1t2T⋅Sdϕdtdt=∫CT⋅Sdϕ,{displaystyle W=int _{t_{1}}^{t_{2}}mathbf {T} cdot {vec {omega }}dt=int _{t_{1}}^{t_{2}}mathbf {T} cdot mathbf {S} {frac {dphi }{dt}}dt=int _{C}mathbf {T} cdot mathbf {S} dphi ,}，其中C是從φ（t₁）到φ（t₂）的運動軌跡。此積分取決於φ（t）的值，因此與路徑相關。

如果轉矩T與角速度矢量一致，那麼可寫成：

T=τS,{displaystyle mathbf {T} =tau mathbf {S} ,}

而且若轉矩和角速度是恆定的，那麼功可寫成這個形式：

W=∫t1t2τϕ˙dt=τ(ϕ2−ϕ1){displaystyle W=int _{t_{1}}^{t_{2}}tau {dot {phi }}dt=tau (phi _{2}-phi _{1})}。

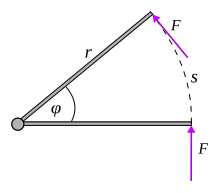
A force of constant magnitude and perpendicular to the lever arm

此結果可以更簡單的理解，如圖所示。這股力將通過圓弧的距離s=rφ，所作的功即是：

W=Fs=Frϕ{displaystyle W=Fs=Frphi }。，導出轉矩τ=Fr，得：

W=Frϕ=τϕ,{displaystyle W=Frphi =tau phi ,}

以上，請注意只有轉矩在角速度矢量方向的部分才有作功。

力与位移

力与位移都是矢量。功是力与位移的内积，為純量。

W=F→⋅d→=Fdcos⁡θ{displaystyle W={vec {F}}cdot {vec {d}}=Fdcos theta }           （1）

其中θ{displaystyle theta }是力矢量和位移矢量的夹角。

为使此式正确，力须为常矢量，路径须为一条直线。

如力随时间变化或路径不为直线，上式不再适用，此时需使用曲线积分。故功的一般公式为：

W=∫CF→⋅dx→{displaystyle W=int _{C}{vec {F}}cdot mathrm {d} {vec {x}}}            （2）

其中

C{displaystyle textstyle _{C}}是路径；

F→{displaystyle {vec {F}}}是力矢量；

x→{displaystyle {vec {x}}}是位移矢量。

表达式δW=F→⋅ds→{displaystyle delta W={vec {F}}cdot mathrm {d} {vec {s}}}是一个非恰当微分，WC{displaystyle textstyle {W_{C}}}与路径有关，求微分后不能得到F→⋅dx→{displaystyle {vec {F}}cdot mathrm {d} {vec {x}}}。

非零力可以不作功，这一点与冲量不同。冲量是力对时间的累积。冲量是矢量，所以圆周运动时虽向心力不作功，但产生了对物体的非零冲量。

力矩

力矩所作功可由下式计算得到：

W=τθ {displaystyle W=tau theta }

其中τ{displaystyle tau }为力矩。

功與動能

功動能定理（The work–kinetic energy theorem）或稱功能定理（The work–energy theorem）、功能原理（The work–energy principle），意指合力作用在物質上（合力作功）的功等於物質的動能變化量

合力W在質點上所作的功等於其動能的變化量Ek{displaystyle E_{k}},^[4]

W=ΔEk=12mv22−12mv12{displaystyle W=Delta E_{rm {k}}={tfrac {1}{2}}mv_{2}^{2}-{tfrac {1}{2}}mv_{1}^{2}},

v1{displaystyle v_{1}} and v2{displaystyle v_{2}}分別是質點的初速度和末速度，m則是質量。

概述

功與能的原理由牛頓第二運動定律推導，其中包括作用在質點上的合力和約束反力對質點造成的位移量。

对于匀变速直线运动的情形，推导如下式。

W=Fd=mad=ma(v22−v122a)=mv222−mv122=ΔEk{displaystyle W=Fd=mad=maleft({frac {v_{2}^{2}-v_{1}^{2}}{2a}}right)={frac {mv_{2}^{2}}{2}}-{frac {mv_{1}^{2}}{2}}=Delta {E_{k}}}，d=v22−v122a{displaystyle d={frac {v_{2}^{2}-v_{1}^{2}}{2a}}}，v22=v12+2ad{displaystyle v_{2}^{2}=v_{1}^{2}+2ad}

一般情况下的推导则如下式。

W=∫t1t2F⋅vdt=∫t1t2Fvdt=∫t1t2mavdt=m∫t1t2vdvdtdt=m∫v1v2vdv=12m(v22−v12){displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt=int _{t_{1}}^{t_{2}}F,vdt=int _{t_{1}}^{t_{2}}ma,vdt=mint _{t_{1}}^{t_{2}}v,{dv over dt},dt=mint _{v_{1}}^{v_{2}}v,dv={tfrac {1}{2}}m(v_{2}^{2}-v_{1}^{2})}。

注释

1. 
   ^ Jammer, Max. Concepts of Force. Dover Publications, Inc. 1957. ISBN 0-486-40689-X. 
   


2. 
   ^ Tipler. 1991: 138. 
   


3. 
   ^ ^3.03.1 Resnick, Robert and Halliday, David. Physics, Section 7-2 (Vol I and II, Combined edition). Wiley International Edition, Library of Congress Catalog Card No. 66-11527. 1966. 
   


4. 
   ^ Hugh D. Young and Roger A. Freedman. University Physics 12th. Addison-Wesley. 2008: 329. ISBN 978-0-321-50130-1. 
   

参考

• 
  Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers 6th ed. Brooks/Cole. 2004. ISBN 0-534-40842-7.  引文格式1维护：冗余文本 (link)
  


• 
  Tipler, Paul. Physics for Scientists and Engineers: Mechanics 3rd ed., extended version. W. H. Freeman. 1991. ISBN 0-87901-432-6. 
  

查 论 编 经典力学 表述形式 矢量力学 分析力学（拉格朗日力学 哈密頓力學） 基础概念 空间 时间 速度 加速度 质量 引力 力矩 參考系 力 力偶 冲量 动量 刚体 角动量 慣性 轉動慣量 能量 动能 位能 虛功 作用量 拉格朗日量 哈密頓量 功 重要理论 牛顿运动定律 胡克定律 牛顿万有引力定律 簡諧運動 達朗貝爾原理 歐拉方程式 哈密頓原理 拉格朗日方程式 最小作用量原理 应用 简单机械 斜面 杠杆 滑轮 螺旋 楔子 輪軸 科学史 发展史 开普勒 牛頓 歐拉 達朗貝爾 哈密頓 赫茲 拉格朗日 拉普拉斯 伽利略 雅可比 諾特 分支 静力学 動力學 運動學 工程力學 天體力學 連續介質力學 統計力學

查 论 编 经典力学国际单位 线性（平动）的量 角度（转动）的量 量纲 — L L2 量纲 — — — T 时间: t s absement（英语：absement）: A m s（英语：meter second） T 时间: t s — 距离: d, 位矢: r, s, x, 位移 m 面积: A m2 — 角度: θ, 角移: θ rad 立體角: Ω rad2, sr T−1 頻率: f s−1（英语：inverse second）, Hz 速率: v, 速度: v m s−1 面積速率: ν, 比角动量（英语：specific angular momentum）: h m2 s−1 T−1 頻率: f s−1（英语：inverse second）, Hz 角速率: ω, 角速度: ω rad s−1 T−2 加速度: a m s−2 T−2 角加速度: α rad s−2 T−3 加加速度: j m s−3 T−3 角加加速度: ζ rad s−3 M 质量: m kg ML2 转动惯量: I kg m2 MT−1 动量: p, 冲量: J kg m s−1, N s（英语：newton second） 作用量: 𝒮, actergy（英语：actergy）: ℵ kg m2 s−1, J s（英语：joule-second） ML2T−1 角动量: L, 角冲量: ΔL kg m2 s−1 作用量: 𝒮, actergy（英语：actergy）: ℵ kg m2 s−1, J s（英语：joule-second） MT−2 力: F, 重量: Fg kg m s−2, N 能量: E, 功: W kg m2 s−2, J ML2T−2 力矩: τ, moment（英语：Moment (physics)）: M kg m2 s−2, N m 能量: E, 功: W kg m2 s−2, J MT−3 yank（英语：List_of_equations_in_classical_mechanics#Dynamics）: Y kg m s−3, N s−1 功率: P kg m2 s−3, W ML2T−3 rotatum（英语：rotatum）: P kg m2 s−3, N m s−1 功率: P kg m2 s−3, W

This page is only for reference, If you need detailed information, please check here